---

Coursera课程Fundamentals of Digital Image and Video ProcessingWeek1,2,3的内容.

LSI系统里的2D Discrete Cosine

之前一直没明白这图是个什么意思,原来它就是个简单的2D离散余弦信号..

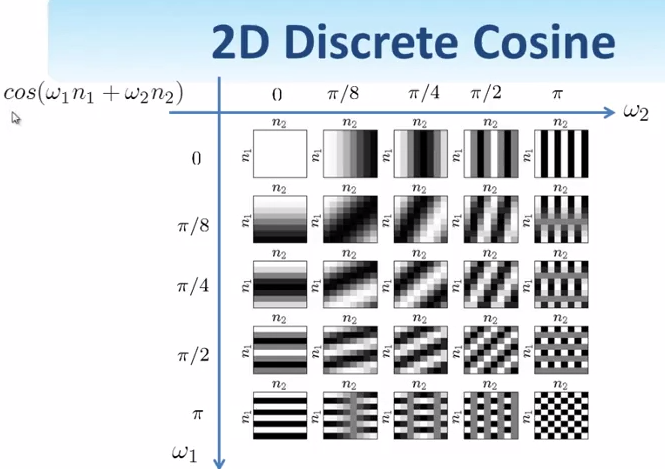
信号是\(cos(\omega_1n_1 + \omega_2n_2)\),\(\omega\)是频率.图中白色代表1,黑色-1,灰色就是(-1, 1)之间的值.
比如左上角第一个图,\(\omega_1 = 0, \omega_2=0\),这时候信号是\(cos(0*n_1 + 0*n_2)\),即\(cos(0) = 1\),所以无论\(n_1, n_2\)取什么值,信号都是1.
第一行第二个图,\(\omega_1 = 0, \omega_2=\pi/8\)时,信号是\(cos(0*n_1 + \pi/8*n_2)\),周期是\(2\pi/\omega_2 = 16\),图上画了半个周期.
其他的都类似了.右下角最后一个,信号在\(n_1\)方向和\(n_2\)方向的周期都是2,在两个方向上都以1,-1交替.
这些小图片就是DCT的基底了.
##2D Convolution
一个脉冲信号经过一个Linear shift-invariant系统,输出叫做系统的脉冲响应.然后,一个信号经过一个LSI系统,系统的响应是这个信号和系统的脉冲响应做卷积的结果.就这张图了.

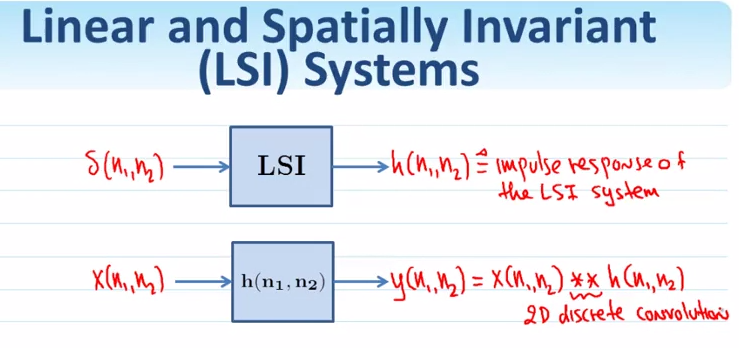
为什么是这样呢?因为..你<<信号系统>>忘光了..
首先,任何一个离散信号都可以表示成下式的卷积形式.

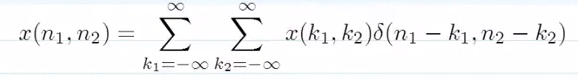
这个式子的意思就是信号分解,比如有一个信号是这个样子.即\(x(-1, 0) = 1, x(0, 0) = 2, x(1, 0) = 3,x(0, 1) = 4 \).

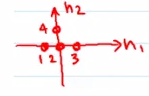
把它拆开看,就是这个图.原信号可以写成不同系数乘以不同位置的脉冲信号再求和的形式.这个系数就是函数值,或者说原信号在某个位置的值.

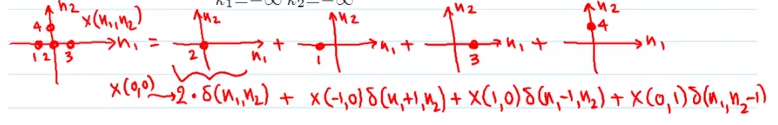
所以把一个信号输入到LSI系统中做变换,可以写乘这个样子.\(x(k_1, k_2)\)可以看成是系数.

这个系统可以看做只对脉冲信号\(\delta\)做了变换(由于是线性系统,系数x可以提到外边去).而对脉冲信号\(\delta\)做变换,系统的输出又叫做脉冲响应\(h\),于是这个式子就变成了原信号\(x\)和脉冲响应\(h\)卷积的形式.

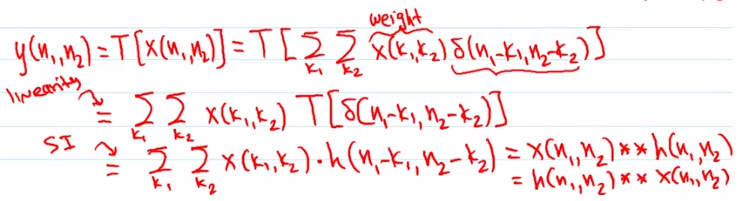
##2D Convolution
一个简单的例子.这两个信号做卷积.

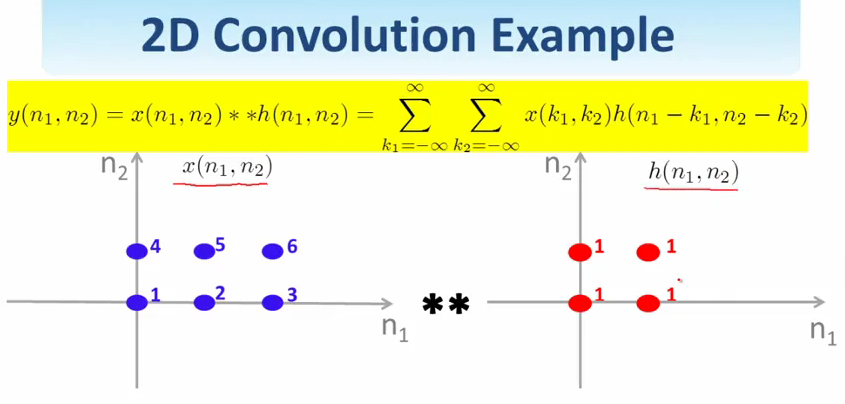
第一步先把其中一个翻转reflection了.

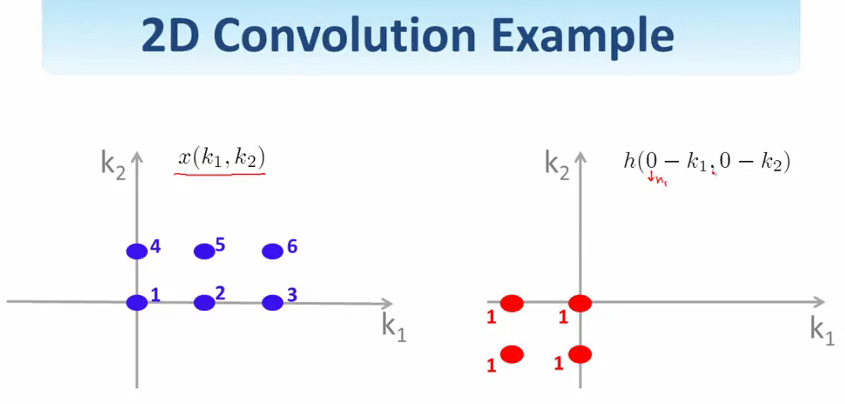
然后选择\((n_1, n_2)\)的值,将两个信号重叠的部分累加起来,得到\(y(n_1, n_2)\)对应的值.






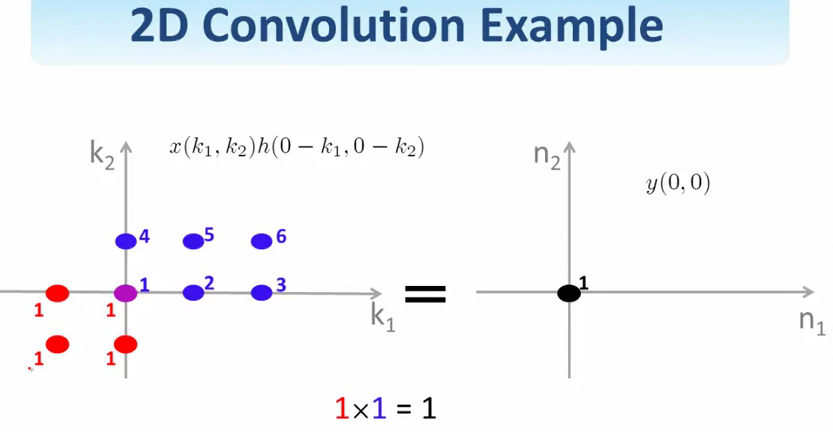
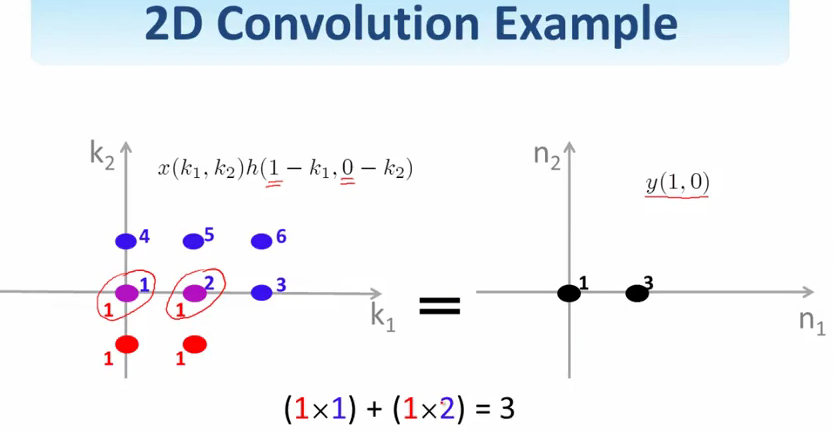
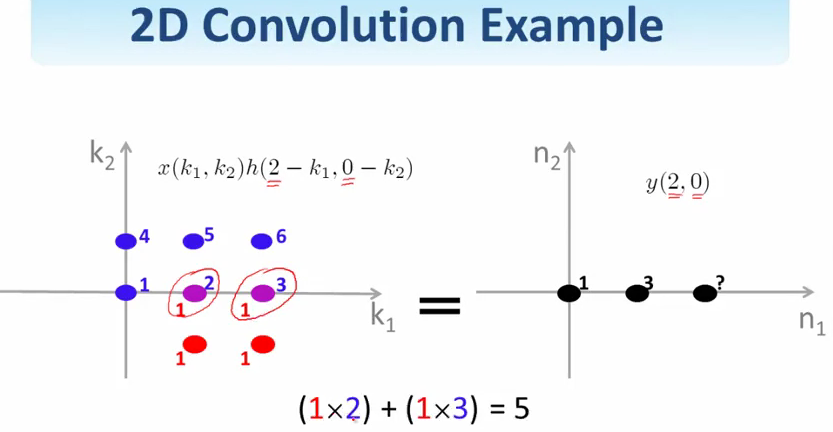
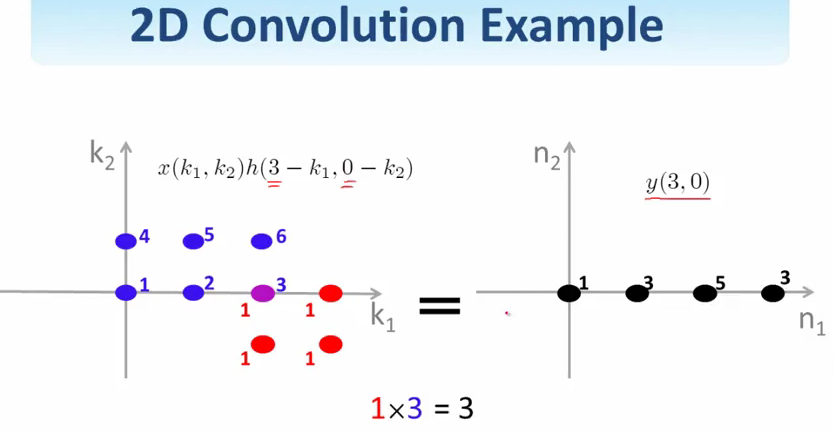
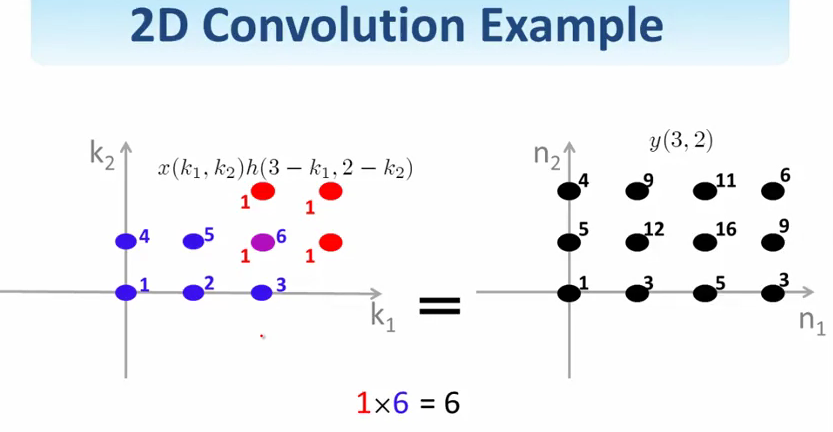
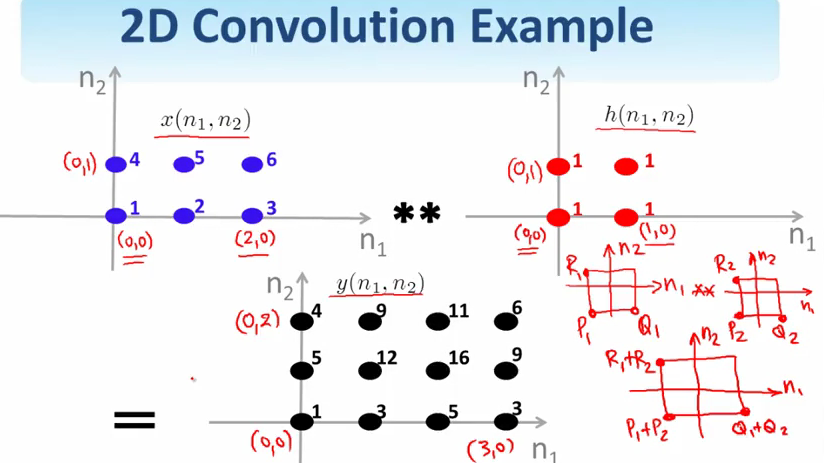
两个信号卷积之后的结果似乎比这两个信号都大一点.具体大多少?
比如\((R_1, P_1, Q_1)\), \((R_2, P_2, Q_2)\)是之前两个信号的左上角,左下角,右下角坐标,那卷积后的信号左上左下右下角坐标就是\((R_1+R_2, P_1+P_2, Q_1+Q_2)\).


2D Fourier Transform
式子.

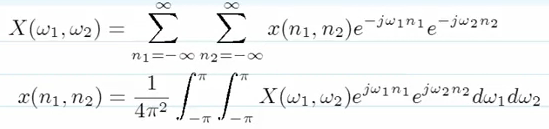
比如要求下图的傅里叶变换.

\(h(0, 0) = 0.204\),\(h(1, 0)\)和\(h(-1, 0)\)可以把复数抵消掉,其他位置也类似.

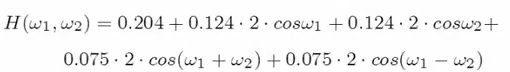
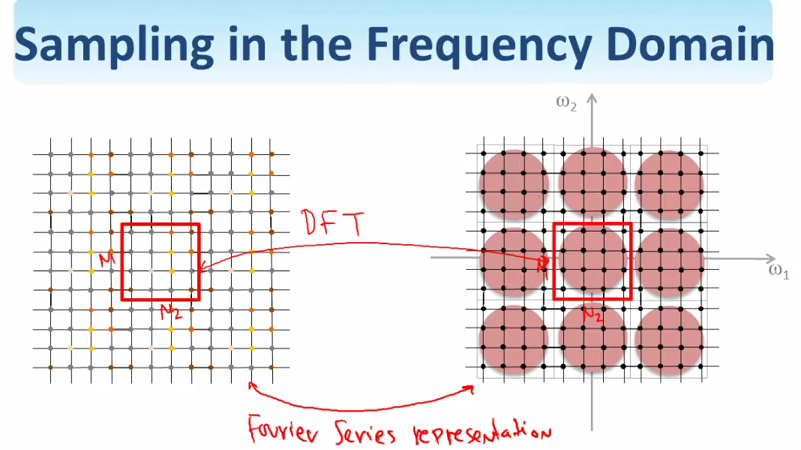
Sampling
上面的傅立叶变换是连续的,在频域.这当然还不够,必须要原信号离散,傅立叶变换也离散才行.
从连续到离散需要采样.首先对一个连续信号做傅立叶变化.如下图.

然后对连续信号进行采样.

对采样点计算傅立叶变化,如下.这里面有两个比较重要的数,\(T_1, T_2\),这是spatial domain的采样周期,式子中的\(\Omega_1T_1\)和\(\Omega_2T_2\)即以前的\(\omega_1\)和\(\omega_2\),\(\Omega\)叫做normalized frequency,单位\(radius/mm\),\(T\)是spatial上的采样周期,单位是mm.反映到频域上,就会发现采样点的傅立叶变换是连续信号傅立叶变换的周期延展,周期是\(2\pi/T_1\)和\(2\pi/T_2\).

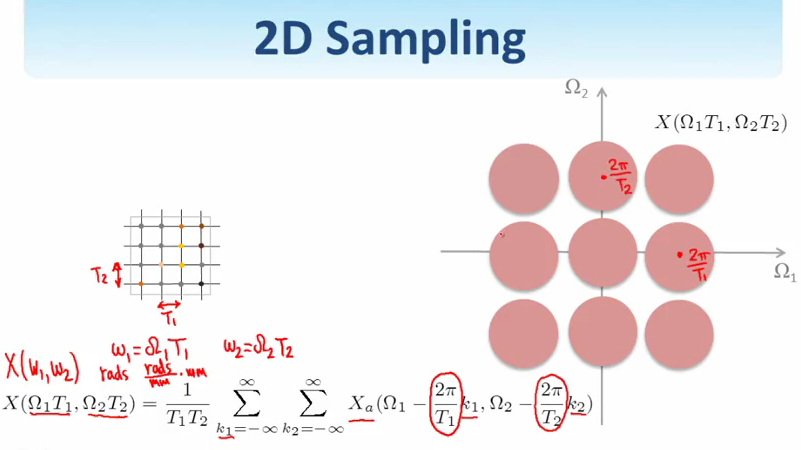
T的大小会直接影响频域信息,T太小无用,T太大则会混叠导致不能恢复信号,这也就是Nyquist定律说的了.


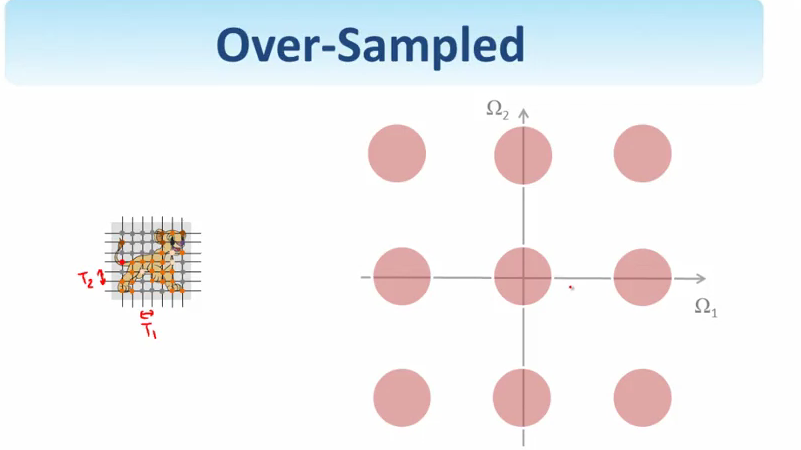
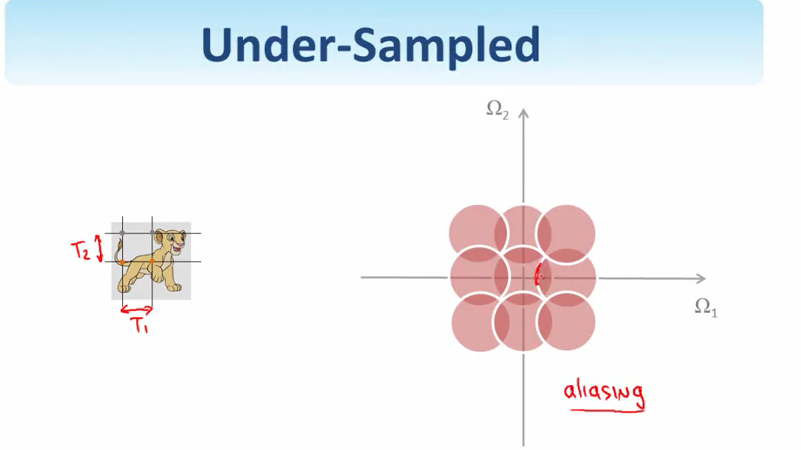
现在频域还是连续的.对频域采样,对应回spatial domain,又变成周期的了,和刚开始的对连续信号进行采样,得到了周期的频域信号一样.同样,在频域的过采样和欠采样也会对应到spatial domain上,欠采样会造成混叠.如下图.周期的离散信号和周期的频域离散信号对应这傅立叶级数,而一个周期的离散信号和一个周期的频域离散信号就是离散傅立叶变换了.