[Algorithms笔记] 归并,选择,插入,希尔,算法稳定性,计算复杂度
Coursera课程Algorithms, Part IWeek2, 3内容.
归并排序
一共3个步骤:
- 将数组分成两部分.
- 递归地对这两部分分别排序(即对这两部分再分).
- 将两个排好序的部分合并.
主要算法就是合并这一步,需要借助一个auxiliary数组和3个位置指针.auxiliary从原数组里复制一份出来,i,j记录两部分起始位置,k作为往进填写的计数器.比较i,j位置上数的大小,把小的填入k,再更新位置.
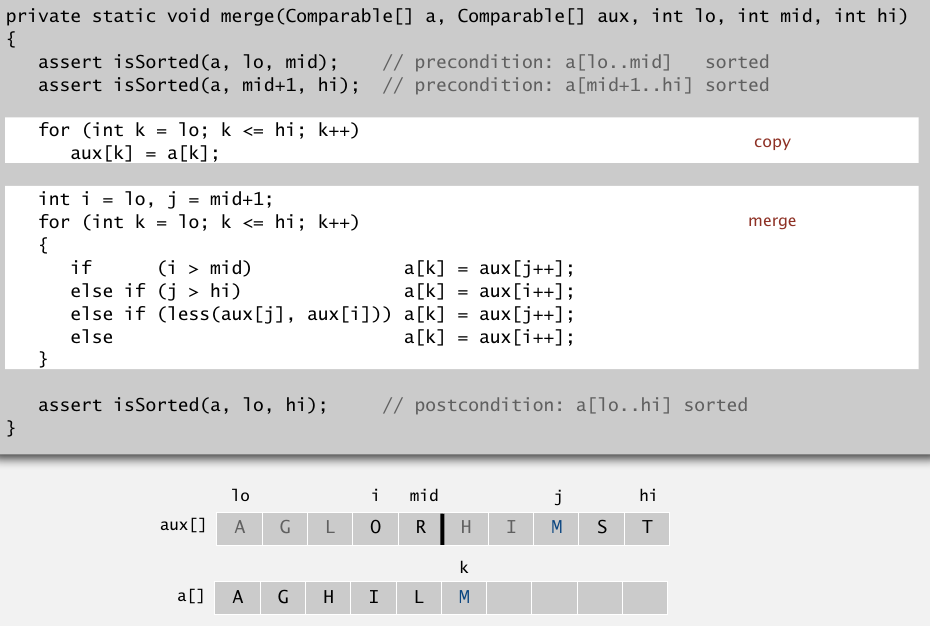
一次排序的执行顺序是这样的.
归并排序的排序发生在合并这一步.对小的子数组,也就是递归到较小的子数组的时候,可以不用归并排序的递归方法来处理的,这时因为子数组很小,可以使用插入排序来处理这个小的子数组.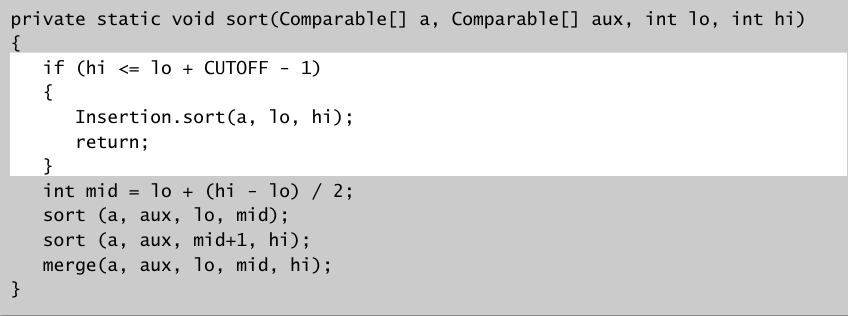
还有一种称为自底向上的归并排序,不需要进行递归,而是经过很多次遍历,每次遍历归并的组的大小乘以2.
比如第一轮只归并相邻两个元素,第二轮4个,第三轮8个.这样需要经过logN轮,每轮归并比较N次,总的时间复杂度基本上还是\(Nlog(N)\).
计算复杂度
之前的\(Nlog(N)\)是指算法需要的操作数的上界,算法还需要证明其有一个下界,表明对一个问题的操作数的下限.上界和下界同一数量级的算法是最优算法.比如对排序问题,要求它的下界,需要用到决策树.

对3个数a,b,c排序,决策树也就是不断提问,问完所有的可能顺序.每个叶子表示一种可能性.
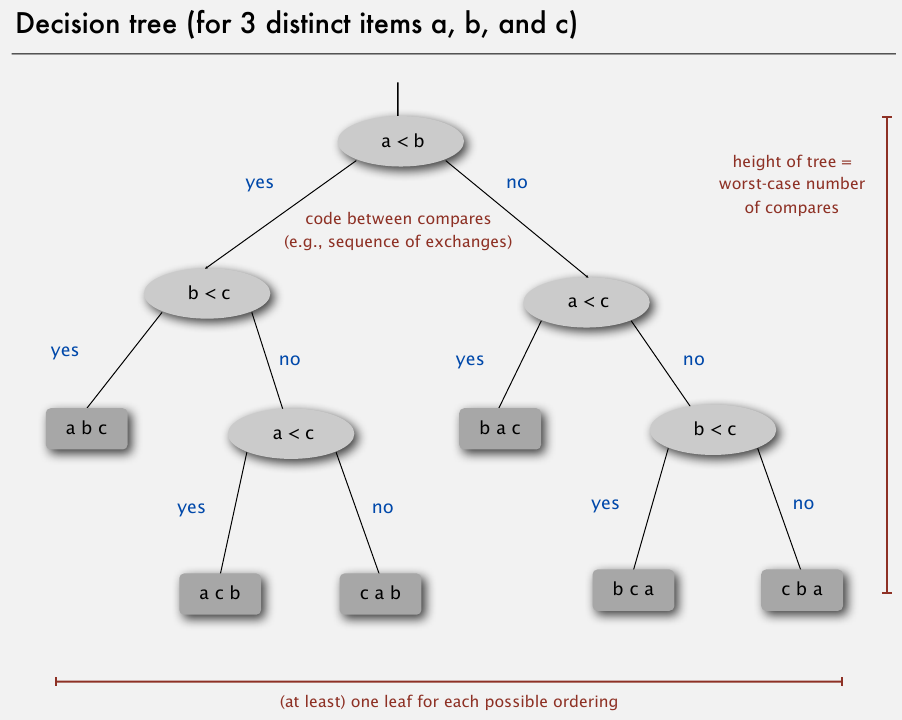
对一个高度h的树(即最多经过h次提问便得到结果,也即h次操作),最多有\(2^h\)个叶子,它大于等于决策树上的叶子数目.对N个数的排序,最多有N!种顺序,所以决策树上最少有N!个叶子.这样可以得到排序问题的下限\(Nlog(N)\).

从比较次数来看,因为归并排序的复杂度上界和下界一样,所以它是最优算法,但从空间使用来看不是,因为它需要多用一个auxiliary数组.
使用Comparators
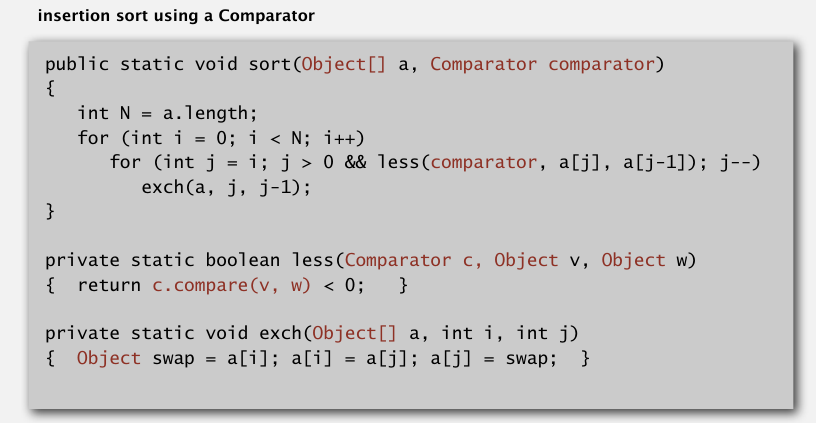
有时候需要多种排序规则,比如字符串数组,可以忽略大小写排序,也可以考虑大小写.这时应该使用Comparator接口.
需要几种比较方法,就实现几个使用Comparator接口的内部类,然后实现compare方法.
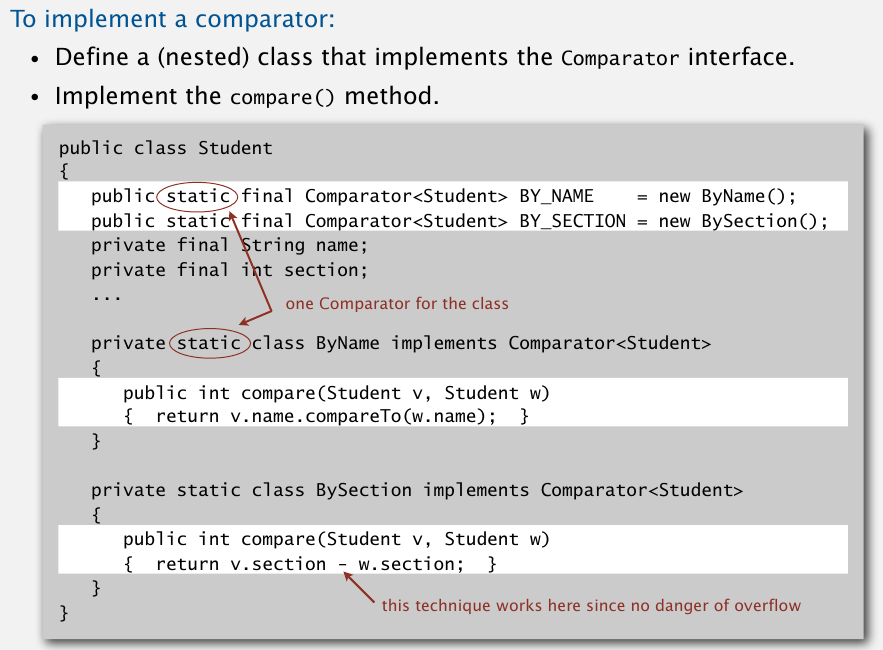
排序的时候把Comparator的对象传进去,使用它的compare方法.
使用Comparable
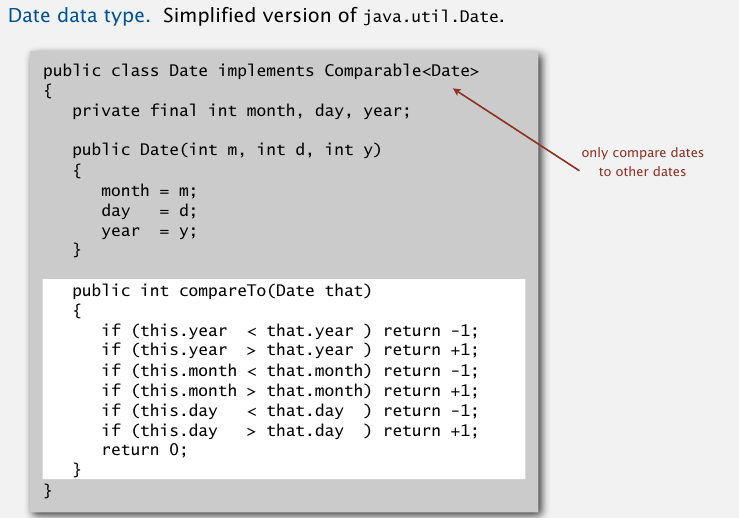
让排序算法对不同的类型都能进行排序,还可以使用Comparable接口.String,Integer已经使用了Comparable接口.
使用方法是,定义类时使用Comparable,实现compareTo方法.
参考http://blog.csdn.net/mageshuai/article/details/3849143.

其他几种排序
选择排序
选择排序,每次从数组里寻找最小的元素交换到最前面(前面那些已经选出来的小元素已经从小到大排列了,不需要动它们).
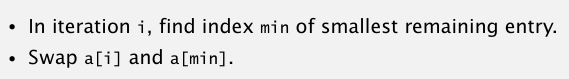
就是每次循环的起始位置往后移.
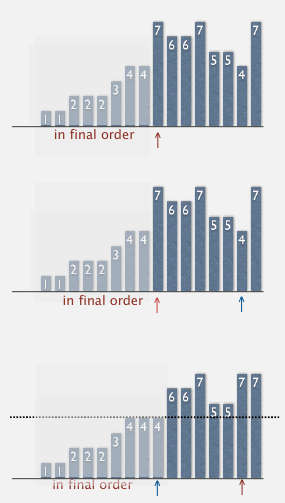
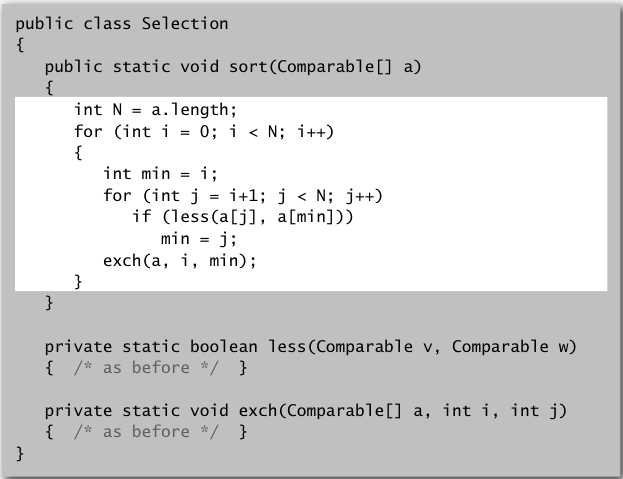
插入排序
每次把当前元素与它左边的元素比较,如果小就交换.这样每次循环中,当前元素的左边都是排好序的.

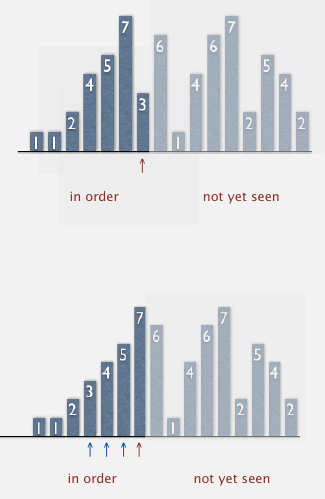
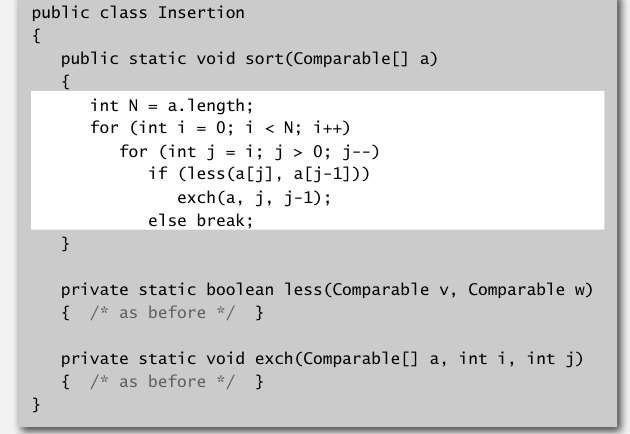
插入排序的最好与最坏情况下需要比较操作的次数.

平均下来就是\(1/4*N^2\).
插入排序有意思的地方是,如果数组是部分排序的,那么插入排序执行时间只是线性增长.
部分排序的定义:

由于插入排序的这个性质,稍微改改就变成了一个更快的排序—-Shell排序.
希尔排序
插入排序中,当前元素只和它前一个元素比较,这样每次只能移动一个位置.希尔排序执行好多组插入排序,但是每组中,当前元素可以和它之前的第h个元素比较交换,这个叫做h-sorting.
这个例子里,先做7-sort,再3-sort,最后1-sort.最后的1-sort就和插入排序是一样的,所以能够得到完全的排序序列,但是由于1-sort处理的数组已经部分排序了,所以它很快.

希尔排序的理论依据:一个g-sorted的数组经过h-sort之后依然保持g-sorted.
如何确定步长?也就是先7,再3,再1?Knuth提出的方法是使用3x+1这个序列.
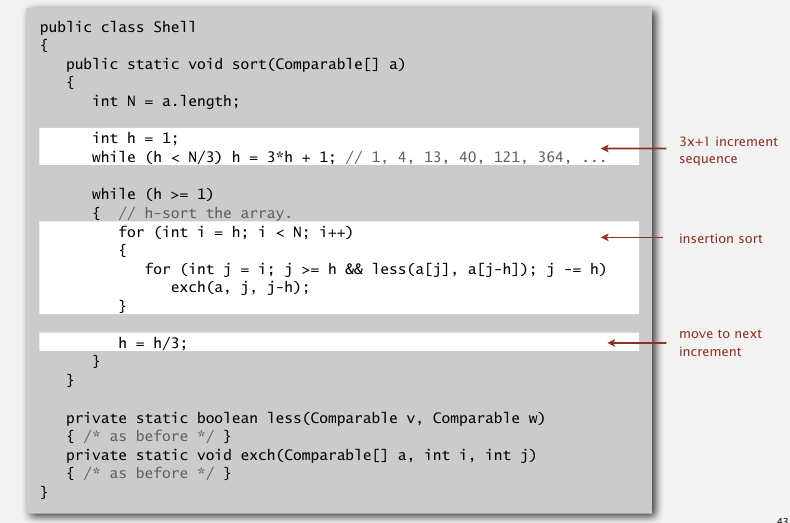
排序算法的稳定性
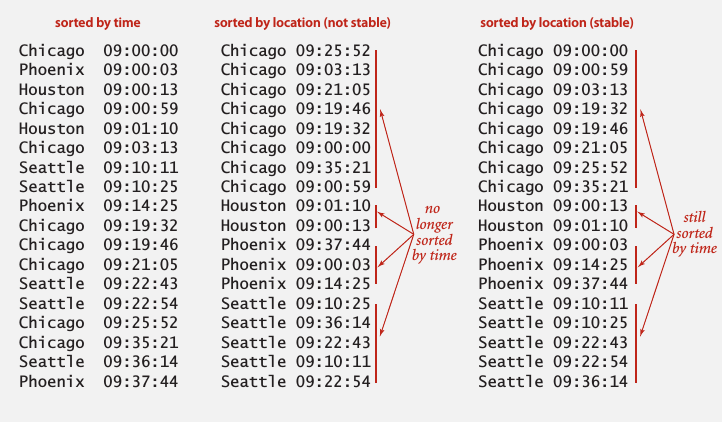
有些需要排序的item有很多属性.下图中首先按照时间排序,再按照地名排序.中间的结果虽然按照地名排序了,但是以前按照时间排的序乱掉了.
右边的结果保留了按时间排序.右边的方法称为稳定的排序.
A stable sort preserves the relative order of items with equal keys.
判断一个排序算法是否稳定,是看排序过程中是否会交换相同属性的元素的位置.
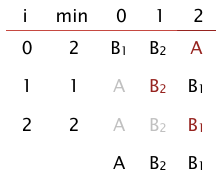
插入排序是稳定的,它每次和相邻的元素比较,只有比相邻元素小时才会发生交换.选择排序是不稳定的,它会发生将相同属性的元素移动的步骤,比如下图,B1,B2相同大小,A比B1,B2小,所以会将B1和A交换,从而B1,B2位置改变.
希尔排序是不稳定的,它会发生长距离的两个元素交换, Long-distance exchange might move an item past some equal item.
归并排序是稳定的,因为它的合并这一步稳定(合并时碰到两个元素相同的情况总是取左边的元素).