[Algorithms笔记] 快速排序,快速查找
Coursera课程Algorithms, Part IWeek2, 3内容.
快速排序
归并排序最重要的一步是合并merge,快速排序最重要的一步称为partition.
Partition是指,随便给一个元素,找到它在整个数组中正确的位置,即在这个位置上,它左边的元素都小于它,右边的元素都大于它.这就是一个元素的正确位置,整个数组排好序后,它还是在这个位置.快速排序就是建立在这个操作上.
先把数组随机打乱,将第一个元素(下标low)作为需要寻找位置的元素,然后用一前一后两个移动指针i,j来寻找位置.
i从左往右,如果a[i]比a[lo]大,就应该停下,因为我们希望的是正确位置左边全比a[lo]小,右边全比a[lo]大,现在a[i]比a[lo]大了,一会肯定要交换到右边去.

j从右往左,碰到a[j]小于a[lo]的停下.

交换a[i], a[j],这样就保证了正确位置左边全小,右边全大(只是我们还没有找到正确位置,还需要接着移动i,j)


直到i,j交叉了,就是i比j大,就该停止了.

这时候交换a[lo]和a[j],刚开始那个元素a[lo]就到了它正确的位置.

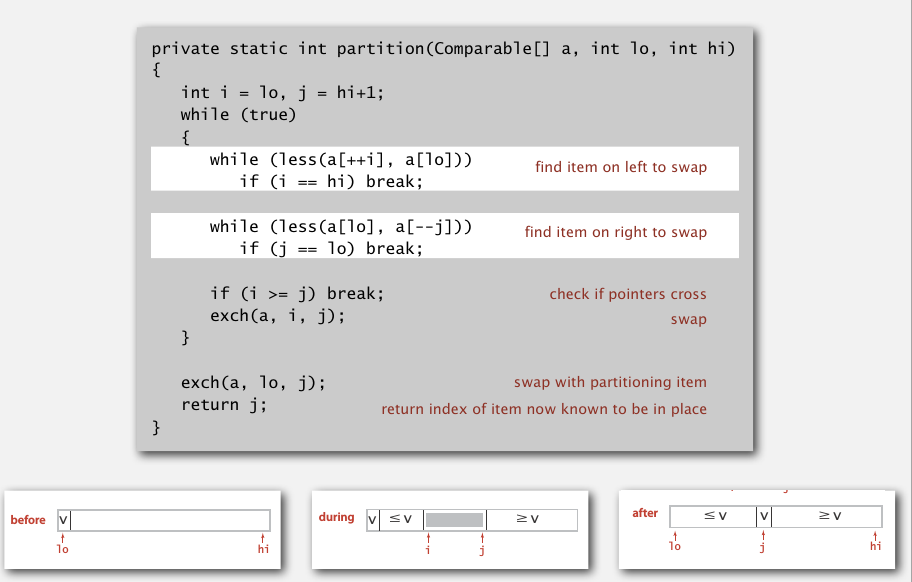
之后就是递归地使用partition了.
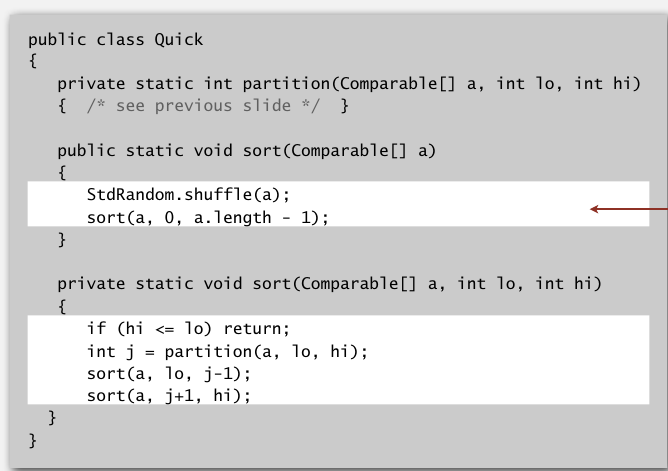
一次快速排序的执行顺序是这样的.随机打乱,进行第一次partition,把a[0]放到合适的位置,然后以这个位置为分割,变成两部分,分别对这两部分进行快速排序.

快排里需要注意的地方很多,比如partition这一步很明显有长距离的元素互换,这样算法就不是稳定的(参考上篇).可以通过增加一个数组的方式来帮助partition更容易,但这样其实开销大.然后如果有数组中有相同大小的元素,如果处理不好快排会变成慢排.还有就是第一步的随机打乱很重要.
快排的best-case需要NlogN次比较操作.它有个反人类的特点就是,如果输入的是一个已经排好序的数组,这个会成它的worst-case,需要\(1/2*N^2\)次比较,因为元素都在正确的位置,partition这一步要不停的比较直到cross.好在算法开始时的随机打乱使得这种情况不不太可能会出现.
改进
合归并排序一样,当递归迭代很深层时,对于已经分割的很小的数组可以不用再递归了,直接使用插入排序处理它们.
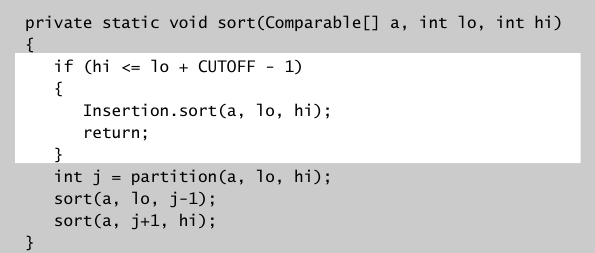
还有当第一次分割越是将数组对半分,快排效果越好,就是第一个partition的元素最好的在排好序的数组的中间.所以可以不取第一个元素作为partition的元素(对于随机打乱的数组,第一个元素平均下来其实也是中间的元素),而是采样3个元素(第一个,中间,最后一个),求它们的中值(不太懂).
快速查找
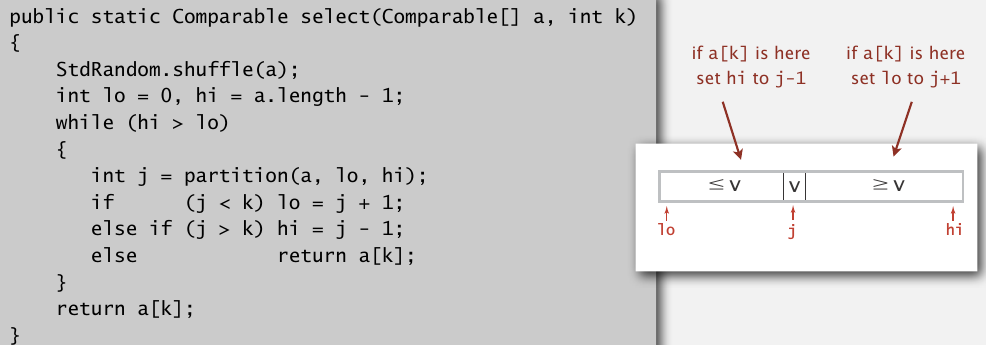
给一个数组,怎么找到第k大的元素?比如最小的元素是第0大,最大的是第N-1大,中间的是第N/2大.可以直接对数组排序,然后找就行了.但是这样用最好的排序方法也需要NlogN.使用快排里的partition,可以使查找算法的计算复杂度变为线性.
想法很简单,首先随机打乱,然后分割,第一次分割可以得到一个元素的正确位置j,并把数组分成j前和j后两部分,这个j实际上就是第j大的元素.然后根据我们要找的第k大元素k,只在j的一边继续partition就行了.
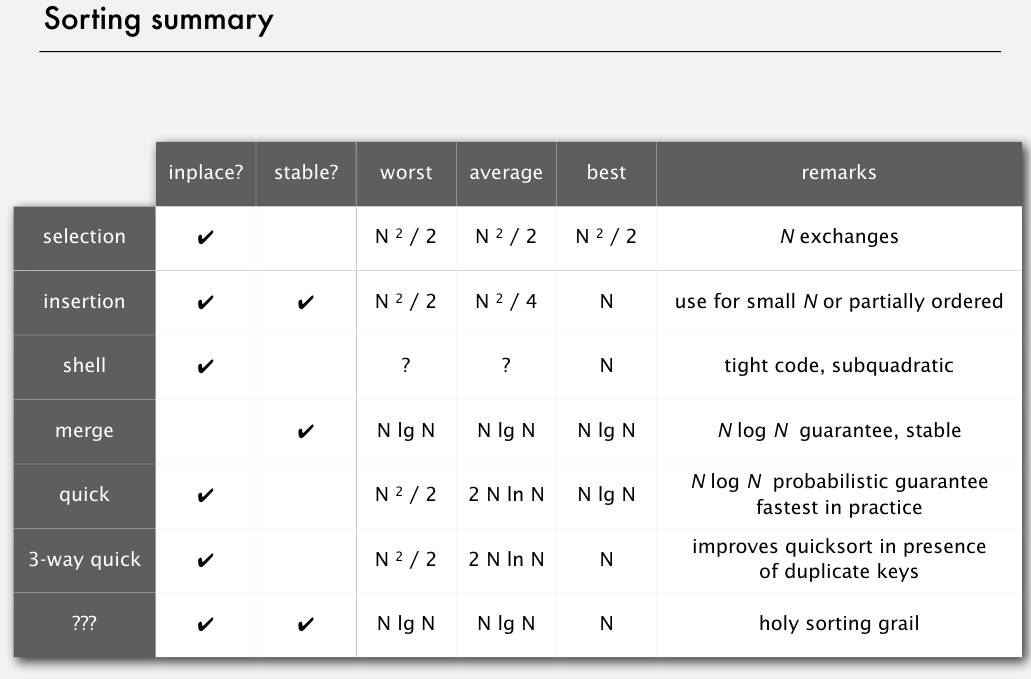
排序算法总结
复杂度二次函数的就不要用了,除了插入排序,在小数组或者部分排序的情况下可以用.
希尔排序是插入排序的升级版,平均操作数目和最多操作书居然是问号..
归并排序又快又有稳定性,只是需要一个额外的辅助数组.
快排算是最好的了.
不,最好的holy sorting grail还是未知的..但排序算法的下限我们已经知道了是NlogN.