[Algorithms] 动态连通性,Union Find,渗透模型,蒙特卡罗采样

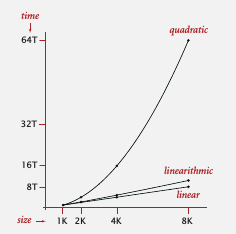
最近在看两个算法课程,一个是北京大学开的算法设计与分析(大妈讲),一个是普林斯顿的Algorithms(大爷讲).普林斯顿的代码讲的比较多,一边讲算法一边讲怎么写API.看了看北大的课程目录,弱弱的不想看了..

以下内容参考自普林斯顿Algorithms Week 1.

连通性问题

两个点之间若存在路径则它们是连通的.从这图里就可以看到这个算法涉及到的一些问题,比如新增加了一条路径,那么很多点的连通性都会改变.图中的点有几个连通区域?像这个图中有两部分.以及,怎么计算连通性.


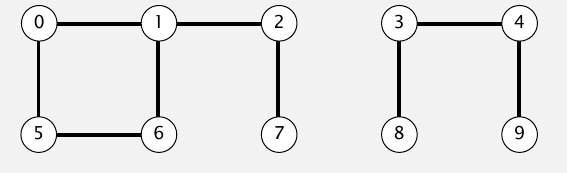
当然除了计算连通性的算法,也需要找出两个点之间的路径的算法.

算法

1.快速查找

最朴素的想法,通过一个数组来记录连通区域信息,属于同一个连通区域的点是连通的.


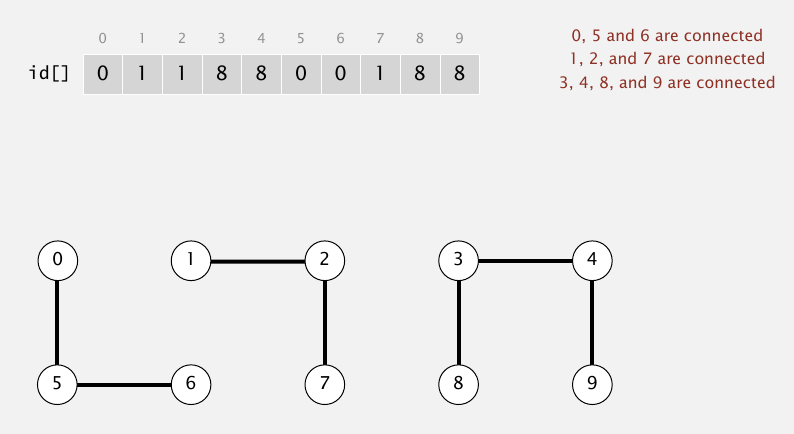
那么当新加入一条路径时,怎么来更新连通区域信息呢?这个更直观了,把两个区域连接在一起,就是把数组里的数字变相同就行.下图中新添加一个1到6的路径,那么1所属的区域就和6所属的区域连通了,都6所属区域的每个点改变信息就行.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
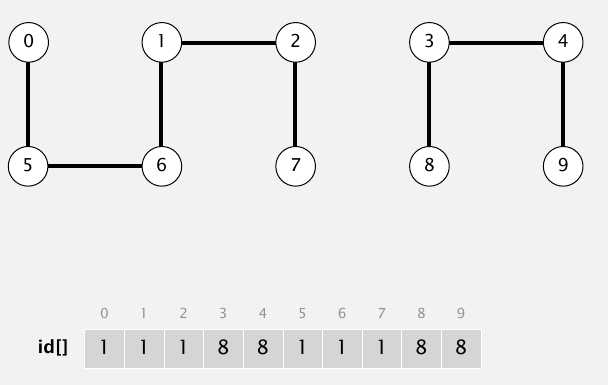
33
package alg.coursera;

public class QuickFindUF {
	private int[] id;

	public QuickFindUF(int N) {
		id = new int[N];
		//初始化,需要操作数组N次
		for (int i = 0; i < N; i++)
			id[i] = i;
	}

	public boolean connected(int p, int q) {
		//判断,需要操作数组2次
		return id[p] == id[q];
	}

	public void union(int p, int q) {
		int pid = id[p];
		int qid = id[q];
//		把p和q连起来,就是把p所属的区域里所有的点记录的区域标号pid
//		全部换成q所属的区域标号qid
//		最多需要操作数组2N+2次		
		for (int i = 0; i < id.length; i++)
			if (id[i] == pid)
				id[i] = qid;
	}
	public void printId(){
		for(int i=0; i<id.length; i++){
			System.out.println(id[i]);
		}
	}
}


这个算法虽然叫快速查找(也叫eager approach),但是它太慢了,在N个点上做N次union操作需要\(N^2\)次数组操作.随着问题规模变大,算法就不能用了.

2.快速连接

上面那个算法主要问题在于连接(union)这一步操作的太多.换一种想法把路径图看成树,如果我们记录的是每个点的父节点信息,因为如果两个点连通,那么它们的父节点的父节点的父节点(根节点)是相同的,这样也可以判断连通性.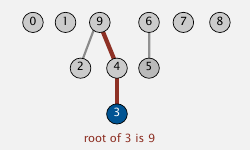

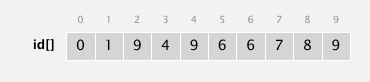
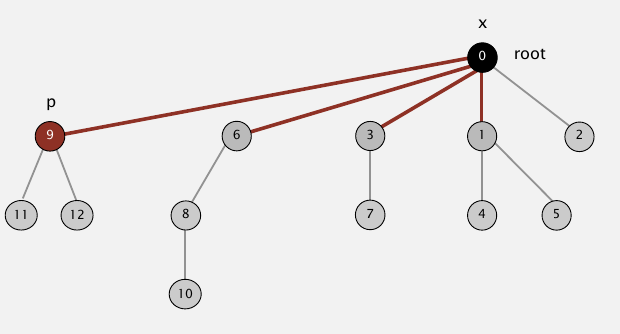
如果要把3和5连接起来,只要把3个根节点和5的根节点连起来.下图中,3个根节点是9,5的根节点是6,只需要修改1处就可以连通两块区域.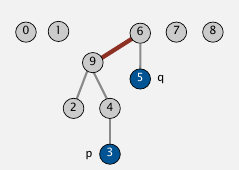

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
package alg.coursera;

public class QuickUnionUF {
	private int[] id;

	public QuickUnionUF(int N) {
		id = new int[N];
		for (int i = 0; i < N; i++)
			id[i] = i;
	}

	private int root(int i) {
		while (i != id[i])//从父节点找根节点,根节点的父节点是它本身,即i==id[i]
			i = id[i];
		return i;
	}

	public boolean connected(int p, int q) {
		return root(p) == root(q);
	}

	public void union(int p, int q) {
		int i = root(p);
		int j = root(q);
		//把p的根节点换成q的根节点
		id[i] = j;
	}
}

这个算法还是慢,树可能太高了,寻找根节点要一层一层往上找.

3.快速连接改进

3.1 加入权值

把p的根节点换成q的,或者把q的换成p的,在上面的算法里是一样的.但如果限定究竟是换哪个,就有可能限制住树的高度,让树不至于过高.改进方法就是通过比较树的大小(即树里的节点的个数,或者树的高度也行),每次都是把较小的树的根节点换成较大的树的根节点.就是这个图了.


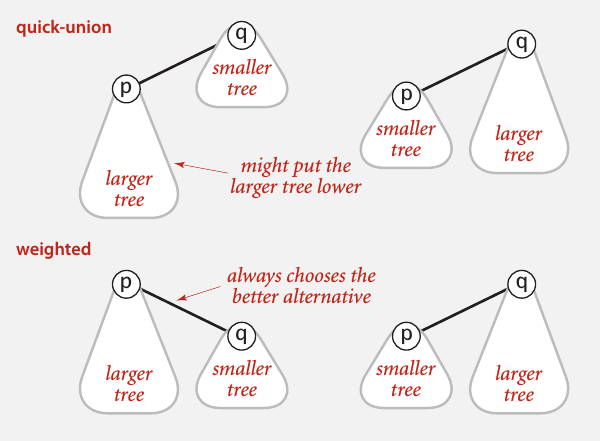
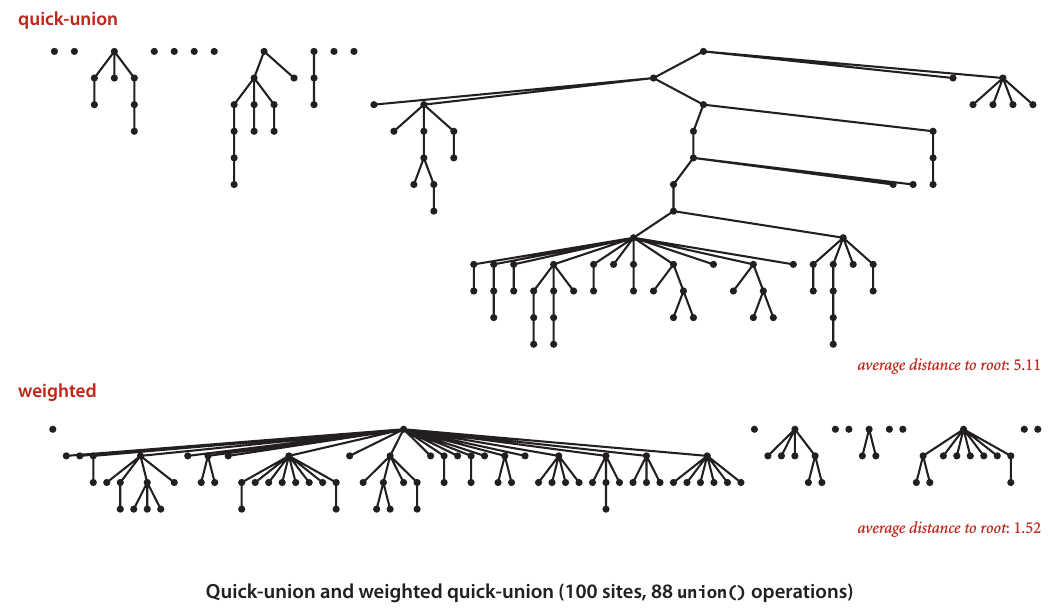
这样做可以得到一个很宽的树,但是都不高.实际上一个节点的最大深度是\(log_{2}N\)

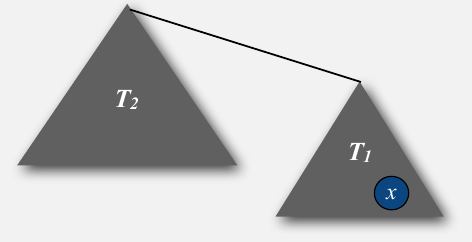
证明呢?这样想,下图中有两个树T1和T2,x是T1中的一个节点.如果把T1的根节点换成T2的,那么节点x的深度就增加1.由于规定了只有当T1比T2小(节点数少)的时候才做这样的操作,所以T1和T2连起来后的大小肯定比T1的一倍还大.我们本来一共有N个节点,假设T1大小是1,连接一次它的大小增加比一倍多,它最多只能增加\(log_{2}N\)次大小就超过N了.所以节点的深度最大也就那么多.

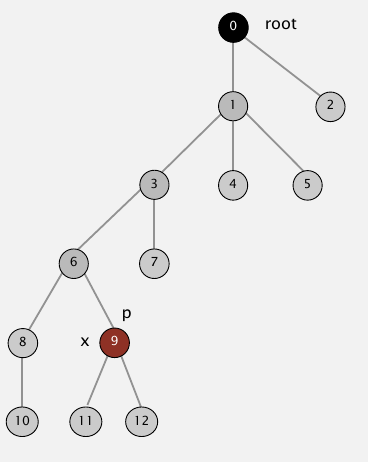
3.2 路径压缩

这个想法是,管它什么父节点呢,反正最后判断和连接时候用的都是根节点,那就在计算p的根节点的时候,把顺着p上去一直走到根节点时遇到的所有节点变成p的根节点,比如找9的根节点的时候,一路上碰到了6,3,1,就把6,3,1的根节点设为9的根节点0.大爷给出这样做的理由有点无语,No reason not to! Keeps tree almost completely flat.


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
//Weighted QuickFindUnionFind with path compression
public class WQuickFindUF { 
	private int[] parent;
	private int[] size; //用来记录每个节点所属于的树的大小
	private int count; //记录有几个连通部分
	
	public WQuickFindUF(int N) {
		parent = new int[N];
		size = new int[N];
		count = N; //开始时互不相连
		for (int i = 0; i < N; i++){
			parent[i] = i;
			size[i] = 1;
		}
	}
    public int count() {
        return count;
    }
	private int root(int i) {
		while (i != parent[i]) {//从父节点找根节点,根节点的父节点是它本身,即i==parent[i]
			parent[i] = parent[parent[i]]; //如果i不是根节点,那么就把i的父节点设为i的祖父节点,也就是往上跳一个
			i = parent[i];
		}
		return i;
	}

	public boolean connected(int p, int q) {
		return root(p) == root(q);
	}

	public void union(int p, int q) {
		int rootP = root(p);
		int rootQ = root(q);
		if(size[rootP] < size[rootQ]) {
			//p小,把p的根节点换成q的
			parent[rootP] = rootQ;
			//这一步相当于把p所在的树加到了q所在的树下,所以q所在的树的大小需要更新
			size[rootQ] += size[rootP];
		}
		else {
			parent[rootQ] = rootP;
			size[rootP] += size[rootQ];
		}
		count--;
	}
}

渗透模型(Percolation)

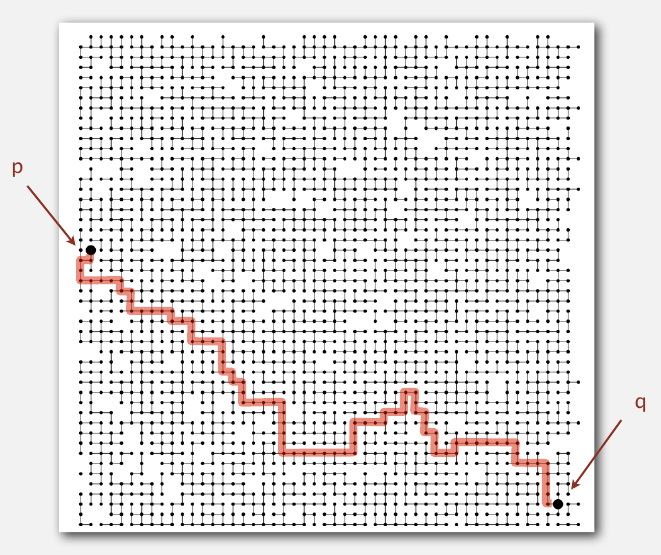
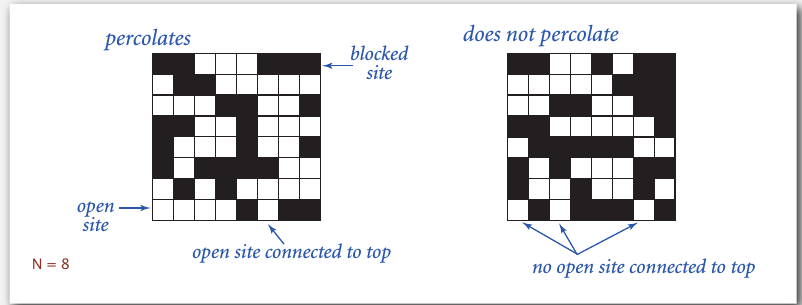
连通性的一个应用就是渗透模型了,下图左边是渗透的,右边不渗透,就是说水能从最上面沿着白孔流到最底,也就是至少在第一行有一个白孔,最底下存在一个白孔,这两个孔是连通的.


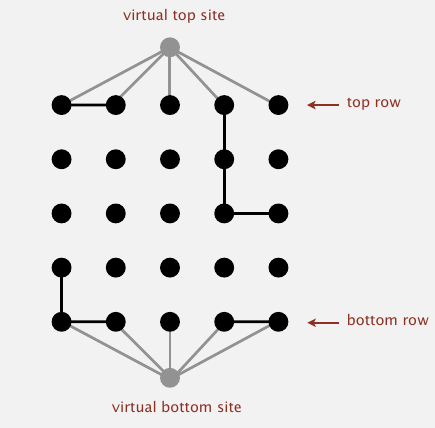
大概比较笨的人都会把问题想成我想的这样吧,正确的做法是多加两个虚拟点(virtual site),如果这个模型是渗透的,那么虚顶点和虚底点就是连通的.然后问题一下子就简单了.


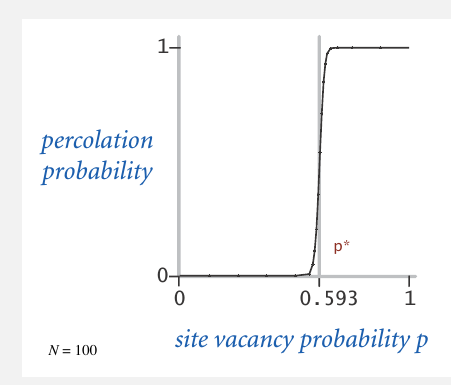
那么一个模型渗透的概率是多少?假设有一个20乘20的模型,它里面的孔是白色(unblocked)的概率是p,黑色(blocked)孔的概率是1-p,那么这个模型渗透的概率是多少?看样子不太好用数学公式描述,事实上它就是不能解的.解决方法是用大量模拟实验(simulation)来找到这个概率,也就是蒙特卡罗采样了.当p比某个值大的时候,模型几乎总是渗透,p比某个值小的时候模型几乎不渗透.这么非线性看来确实不好用数学公式描述.


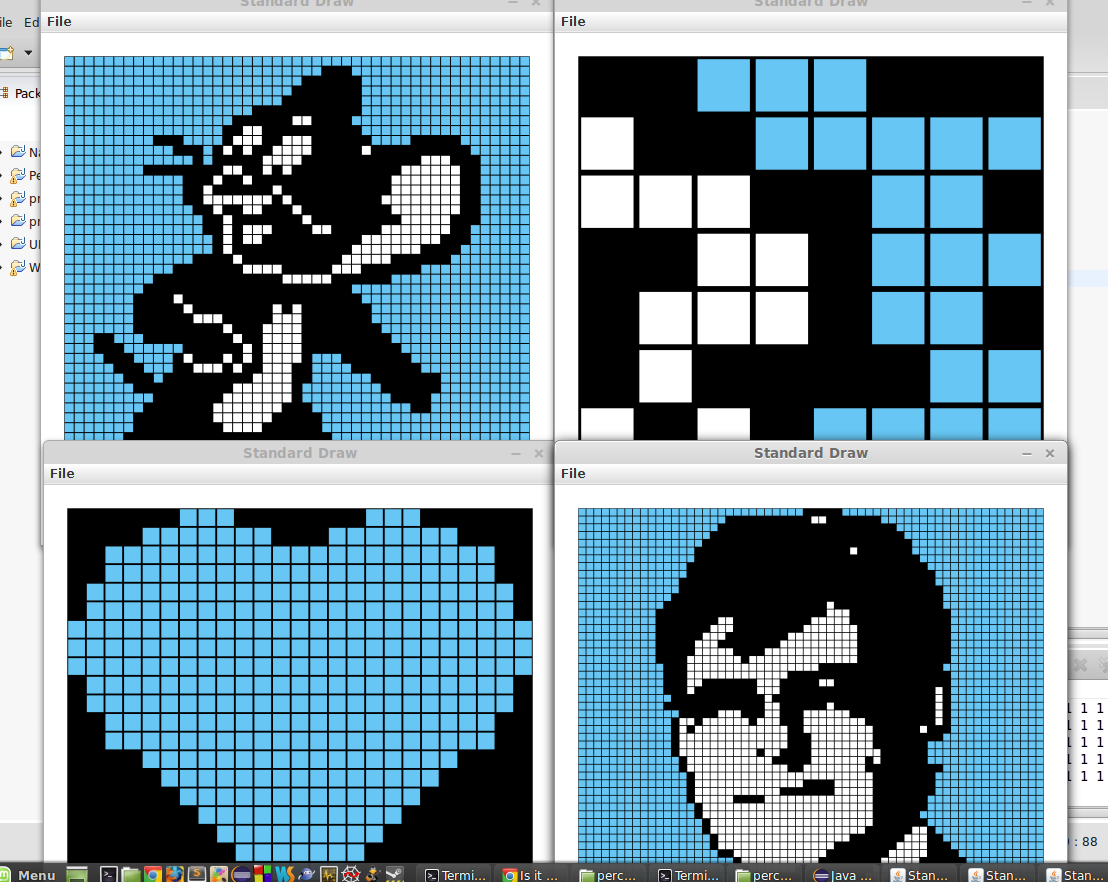
渗透模型和模拟实验的代码很简单,我写了一个原始的版本,啥错误处理都没,不过能用.这几个图是提供的原始输入文件画出来的(右下角就是那大爷..年轻时候吧).蓝色代表这些点是和最顶上连着的,水能渗透过来.

最后

讲这门课的大爷除了写了本Algorithms,还写了本Introduction to Programming in Java: An Interdisciplinary Approach.我翻到这大爷给学生们留的编程作业时就坐不住了,尼玛要是我大二时知道这大爷就好了.第一个作业就是Guitar Hero,往中间翻了翻还有Mozart Waltz Generator,这难道是我高中那会混迹有意思吧时看到的那个??!!