之前的MNIST每张图片大小只有28*28,所以把它展成大小为784的向量作为输入还能计算.

但如果图片稍微大点,比如96*96,就相当于有大概\(10^4\)个输入值,如果隐藏层是100,那就有\(10^6\)个参数,不管是前馈还是BP都会很慢.

解决办法是不能再把整个图像展开成一个向量作为输入了,这样的做法叫做全连接.如果使用一个局部的接收域(receptive field),用这个小的接收域在大图像上移动,就解决了输入过大的问题.那卷积是什么意思?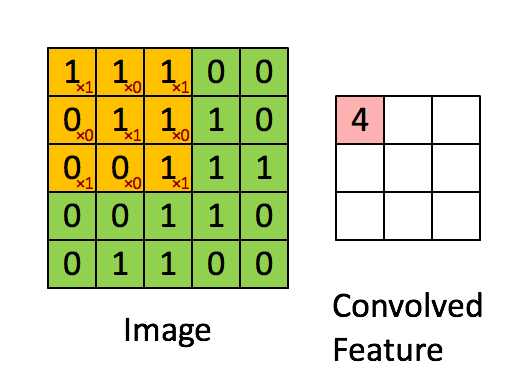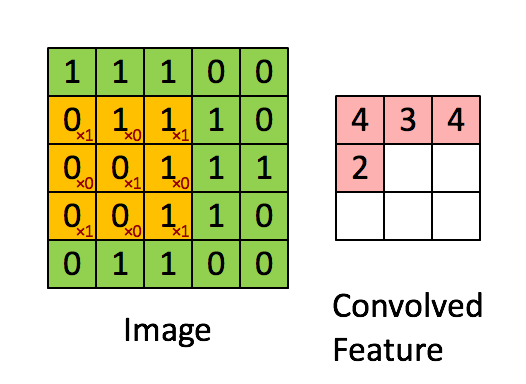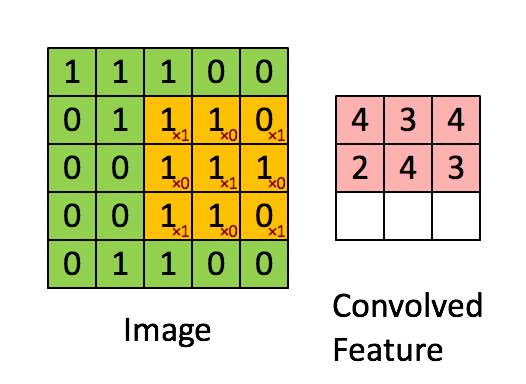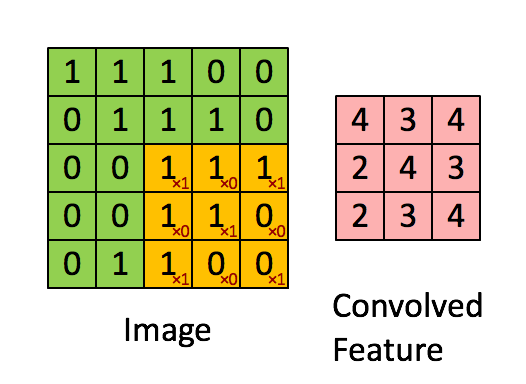

上面这个图,体现出了接收域和卷积的意思.左边5*5的大矩阵就是输入的大图像,中间移动的3*3小矩阵就是接收域.接受域不停移动,在输入图像的每一块上计算(把接受域想象成一个滤波器,这个计算就是用滤波器去乘以图像再求和),这个过程就是卷积.可与看到用这个方法把5*5的原始图像变成了3*3的一个特征.

接受域对应的这个滤波器是怎么来的?在UFLDL之前的教程上,我们从96*96的大图片数据集里随机找了100k个8*8的小图片,用autoencoder训练了这些小图片(输入3*8*8,中间层400个神经元),于是中间这400个神经元就可以看作是小图片的特征了(也就是大图片的精细特征),每一个特征的参数都是3个8*8的矩阵.所以我们可以用这些训练好的8*8矩阵作为接收域的滤波器,用卷积的方法去提取输入图片上的特征(比如接受域的特征代表的意思是某个方向的一条线,那用卷积的方法就可以在输入图像找依次寻找这个方向的线.).

假设某一个通道,输入图像是64*64,用8*8的接收域滤波器去卷机,得到的结果是57*57的矩阵(根据卷积的性质来的).卷积神经网络的第二步叫做pooling,用来进一步降低数据维度.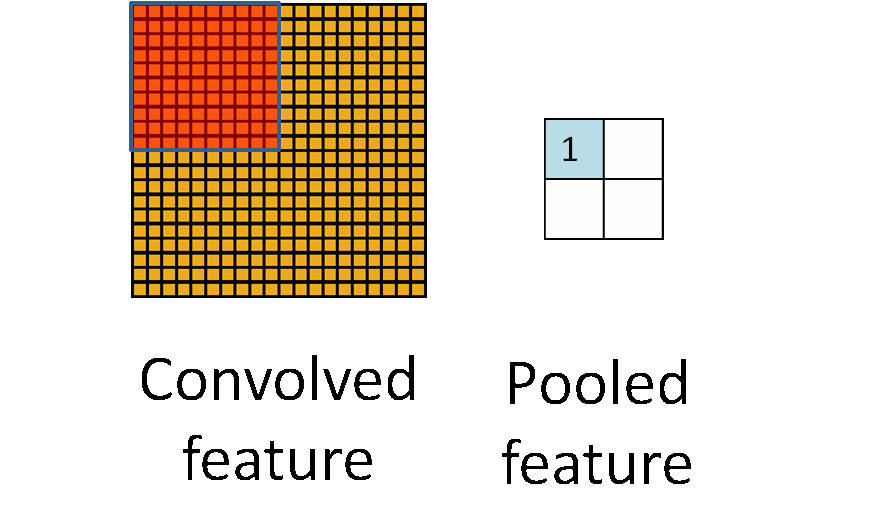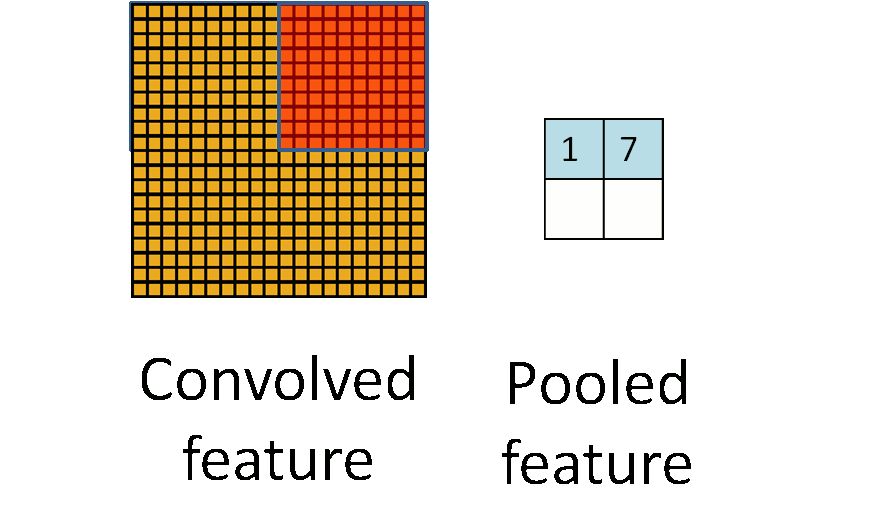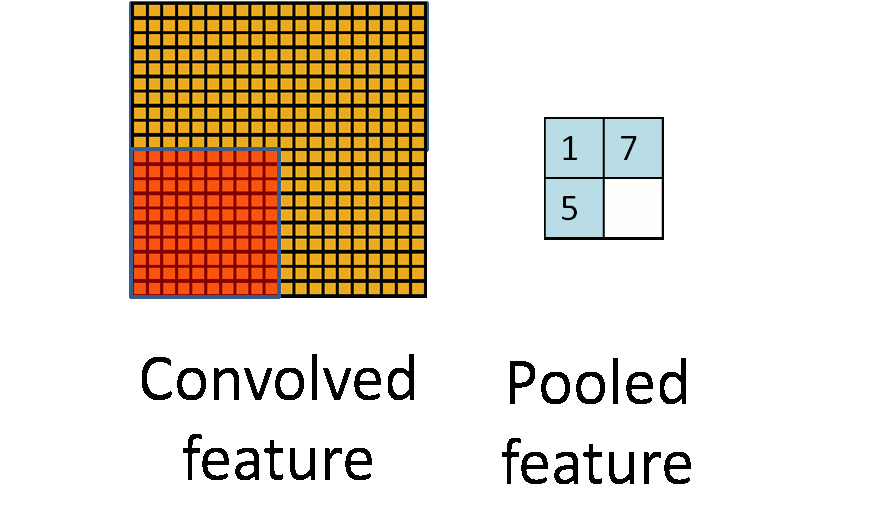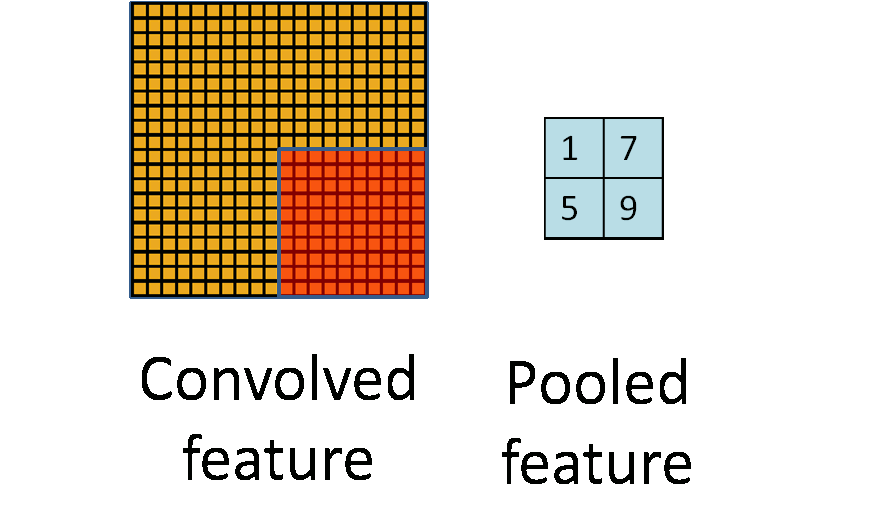

这张图就是pooling的意思,从一块区域中选择一个最大值,或者求平均值,总之就是把一块区域变成了一个数.Pooling可以带来很多很好的特性,比如translation invariant.