2015-10-18

曲线拟合还是分布拟合

---

一堆数据,想要知道是从哪个分布来的,或者想知道所来自的分布的参数,一般要用拟合来确定.曲线拟合和分布拟合都能做到这个,不过有一点差别.

曲线拟合

曲线拟合适用于这样一种情况,数据来自某种采样,比如给定了一组x和对应的f(x),可以用这两组对应的数据来拟合曲线.这里的输入数据必须是成对的,即一个x对应一个f(x).
Matlab文档里有这么一个例子,想要拟合出血液中某物质的浓度随时间变化的曲线(分布).输入数据是时间和对应时间上的浓度采样.

time = [ 0.1   0.1   0.3   0.3   1.3   1.7   2.1   2.6   3.9   3.9 ...
         5.1   5.6   6.2   6.4   7.7   8.1   8.2   8.9   9.0   9.5 ...
         9.6  10.2  10.3  10.8  11.2  11.2  11.2  11.7  12.1  12.3 ...
        12.3  13.1  13.2  13.4  13.7  14.0  14.3  15.4  16.1  16.1 ...
        16.4  16.4  16.7  16.7  17.5  17.6  18.1  18.5  19.3  19.7];
conc = [0.01  0.08  0.13  0.16  0.55  0.90  1.11  1.62  1.79  1.59 ...
        1.83  1.68  2.09  2.17  2.66  2.08  2.26  1.65  1.70  2.39 ...
        2.08  2.02  1.65  1.96  1.91  1.30  1.62  1.57  1.32  1.56 ...
        1.36  1.05  1.29  1.32  1.20  1.10  0.88  0.63  0.69  0.69 ...
        0.49  0.53  0.42  0.48  0.41  0.27  0.36  0.33  0.17  0.20];

并且知道,这个分布是Weibull分布,形式如下.

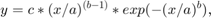
然后就能拟合了,需要手写出分布方程,再把初始参数和数据输进去.

modelFun =  @(p,x) p(3) .* (x ./ p(1)).^(p(2)-1) .* exp(-(x ./ p(1)).^p(2));
startingVals = [10 2 5];
coefEsts = nlinfit(time, conc, modelFun, startingVals);

验证拟合的好坏是画出曲线,计算对应点的误差,求和.

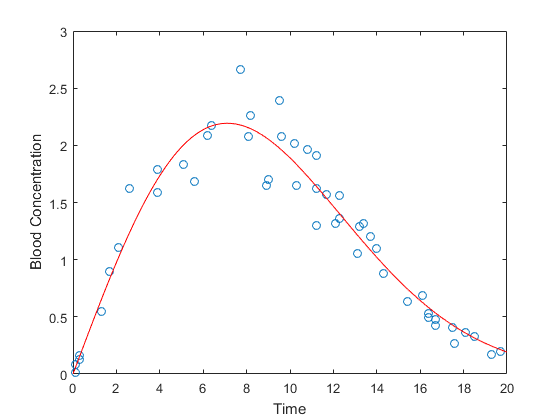
分布拟合

分布拟合适用于这样一组情况,数据只有采样值而没有对应的时间值,只有一个轴图都没法画,只能统计.Matlab文档里的例子是这样,拟合50个电子元件寿命的分布.输入数据只有f(x).

life = [ 6.2 16.1 16.3 19.0 12.2  8.1  8.8  5.9  7.3  8.2 ...
        16.1 12.8  9.8 11.3  5.1 10.8  6.7  1.2  8.3  2.3 ...
         4.3  2.9 14.8  4.6  3.1 13.6 14.5  5.2  5.7  6.5 ...
         5.3  6.4  3.5 11.4  9.3 12.4 18.3 15.9  4.0 10.4 ...
         8.7  3.0 12.1  3.9  6.5  3.4  8.5  0.9  9.9  7.9];

在拟合分布前,想要看看数据的样子,最简单的方法是直方图,直方图在某种程度上已经说明了分布的形状.

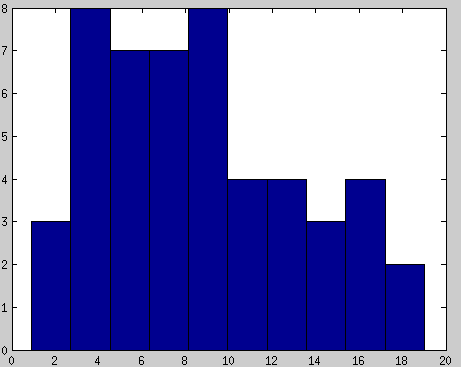
那么是不是可以这样来拟合,x是直方图中各个bin的中心,f(x)是对应bin的高度,用上面曲线拟合的办法计算?好像不错,但缺点很多,具体参考http://www.mathworks.com/help/stats/examples/curve-fitting-and-distribution-fitting.html#zmw57dd0e1798.
分布拟合最常用的办法是最大似然估计MLE,给数据和方程就能算出符合ML的参数.电子元件寿命还是服从Weibull分布,可以用自带的wblfit来拟合.

paramEsts = wblfit(life);

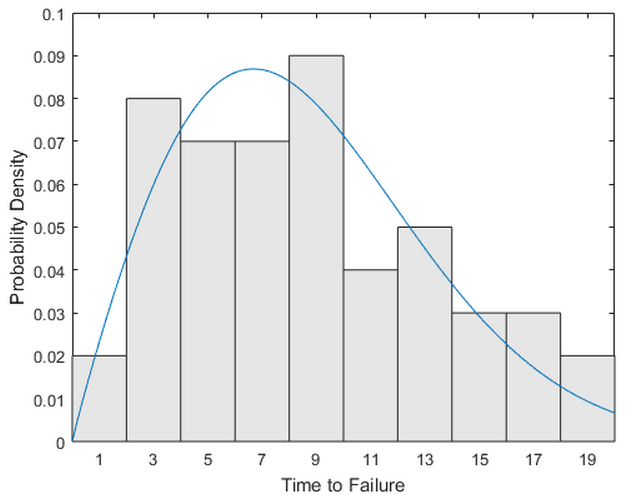
Matlab提供了一些写好的分布拟合函数,用的都是MLE,对于其它分布就要自己用MLE写了.

Whatyouknowabout

Fitting