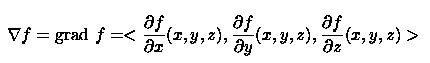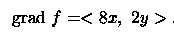画一个函数的梯度

函数的梯度公式如下.


公式来自这里.
当然,这是三个变量的公式,多个变量形式一样.
比如函数\(z = 4*x^2 + y^2\),梯度如下.


梯度一个方向向量,指向函数增长最大的方向.
下面这个程序可以画出一个二元函数的梯度.MATLAB里应该内置了这个功能的函数.
比如方程\(z = 4*x^2 + y^2\),这个函数是一个抛物面.


这是等高线.画了上面带圈点的梯度方向级大小.


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
function main()
close all
% draw 3d 
[XX, YY] = meshgrid([-3:0.1:3], [-3:0.1:3]);
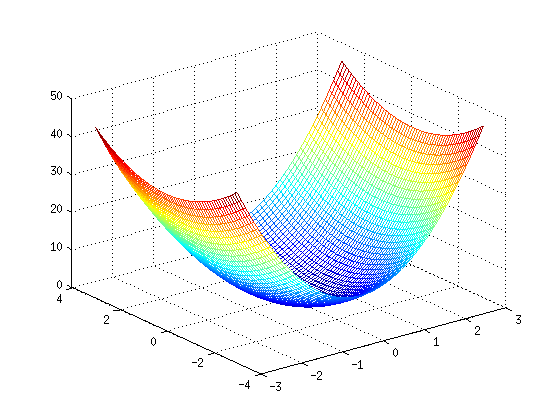
ZZ = 4*XX.^2 + YY.^2;
figure, mesh(XX,YY,ZZ)
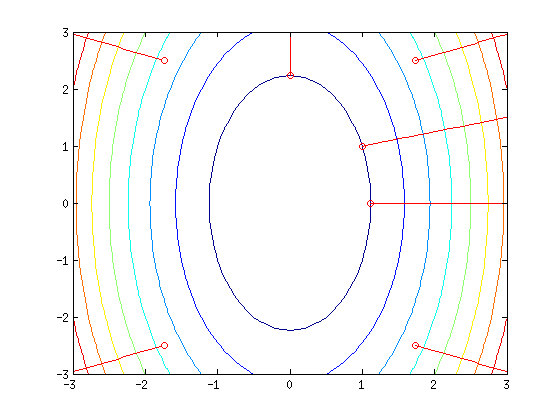
figure, contour(XX,YY,ZZ), hold on
% points
x=1; y=1;
z = poly_func(x, y);
[g_x, g_y] = grad_poly_func(x, y);
draw_gradient(x, y, g_x, g_y)

x=0; y=sqrt(5);
z = poly_func(x, y);
[g_x, g_y] = grad_poly_func(x, y);
draw_gradient(x, y, g_x, g_y)

x=sqrt(1.25); y=0;
z = poly_func(x, y);
[g_x, g_y] = grad_poly_func(x, y);
draw_gradient(x, y, g_x, g_y)

x=sqrt(3); y=2.5;
z = poly_func(x, y);
[g_x, g_y] = grad_poly_func(x, y);
draw_gradient(x, y, g_x, g_y)

x=-sqrt(3); y=2.5;
z = poly_func(x, y);
[g_x, g_y] = grad_poly_func(x, y);
draw_gradient(x, y, g_x, g_y)

x=-sqrt(3); y=-2.5;
z = poly_func(x, y);
[g_x, g_y] = grad_poly_func(x, y);
draw_gradient(x, y, g_x, g_y)

x=sqrt(3); y=-2.5;
z = poly_func(x, y);
[g_x, g_y] = grad_poly_func(x, y);
draw_gradient(x, y, g_x, g_y)

end
function z = poly_func(x, y)
% polynomial z = 4*x^2 + y^2
    z = 4*x^2 + y^2;
end
function [g_x, g_y] = grad_poly_func(x, y)
% gradient of polynomial z = 4*x^2 + y^2
    g_x = 8*x;
    g_y = 2*y;
end
function draw_gradient(x, y, g_x, g_y)
% draw gradient.
% you need to make your figure hold on first.
% Si, 2015-05-21
    plot(x,y,'ro')
    if g_x ~= 0 && g_y ~= 0
        ang_tan = g_y/g_x;
        if g_x > 0
            horizontal_x = [0:0.1:g_x];
        else
            horizontal_x = [g_x:0.1:0];
        end
        horizontal_y = horizontal_x*ang_tan;
        plot(horizontal_x+x, horizontal_y+y, 'r-');  
    else
        if g_x == 0
            if g_y > 0
                horizontal_y = [0:0.1:g_y];
            else
                horizontal_y = [g_y:0.1:0];
            end
            horizontal_x = 0*horizontal_y;
            plot(horizontal_x+x, horizontal_y+y, 'r-');
        end
        if g_y == 0
            if g_x > 0
                horizontal_x = [0:0.1:g_x];
            else
                horizontal_x = [g_x:0.1:0];
            end
            horizontal_y = 0*horizontal_x;
            plot(horizontal_x+x, horizontal_y+y, 'r-');
        end
    
    end
end