fft又忘了咋用了?

(fft就是比dft快点,所以在这就把fft和dft看做一个意思不区分了)

首先,来生成一个离散正弦信号(其实这一步我也忘了咋用了!)

第一种生成方法来自基本的正弦公式

\(x = sin(\omega t) \) or \(x = sin(2\pi f t) \) 一个角频率一个频率.

离散情况下,就要用到采样率fs来表示上面那个时间t.比如,要生成一个频率是110HZ的正弦波,首先需要知道要多少个点是吧?假设一共要生成N=1000个点.采样率的意思就是1秒钟有多少个点(或者说1秒钟对应到离散情况下为多少点).离散点坐标为n = [1, 2 ,…, N],转化成时间序列t = n / fs.如果fs = 1000的话,这个t刚好就是0到1秒(分成了1000份).

然后就能按照上面的正弦信号公式来生成离散正弦信号了.

\(x = sin(2\pi*f*n/fs)\)

第二种生成方法直接写出来再解释.

\(x = sin(2\pi*k*n/N)\)

还是假设要生成N = 1000个点,n和上边一样是[1, 2, …, N],这样式子里的\( 2\pi*n/N \)刚好就是从0到\(2\pi\).然后k很明显代表的就是频率了..如果k = 110, 那么\( 2\pi*k*n/N \)就取了110个 \(2\pi\),即110个周期,所以它的频率就是110HZ.这种生成方法没有提到采样率fs.

进行fft时,一定要记着把结果对应到正确的频率上.

用上面生成的x,直接做fft

1
2
3
4
5
6
7
8
N = 1000
f = 110
fs = 1000
x = numpy.sin(2*numpy.pi*f*numpy.arange(N)/fs)
X = numpy.fft.fft(x)
magX = numpy.abs(X)
plt.plot(magX[:N/2]) #只取正频率
plt.show()

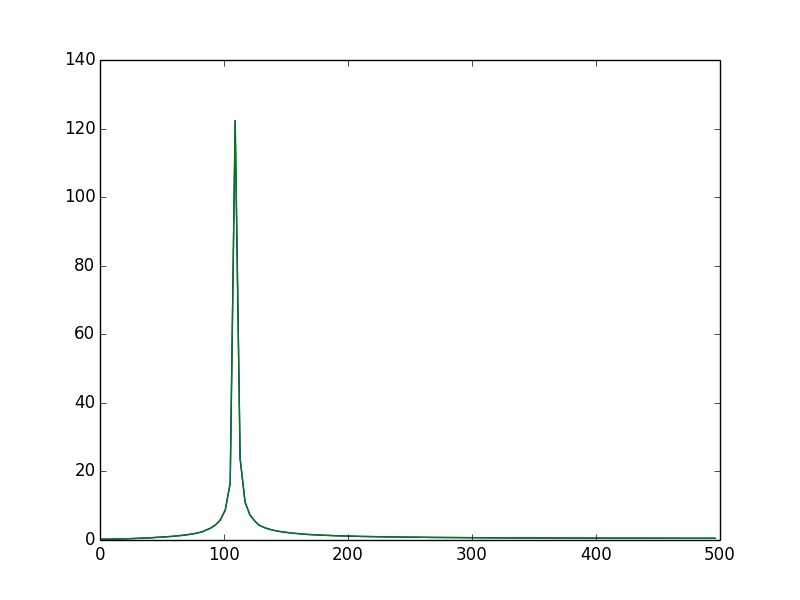
这样是对所有的x(1000个点)做了fft,得到的频谱幅度值magX频率是正确的.在110HZ上有个脉冲.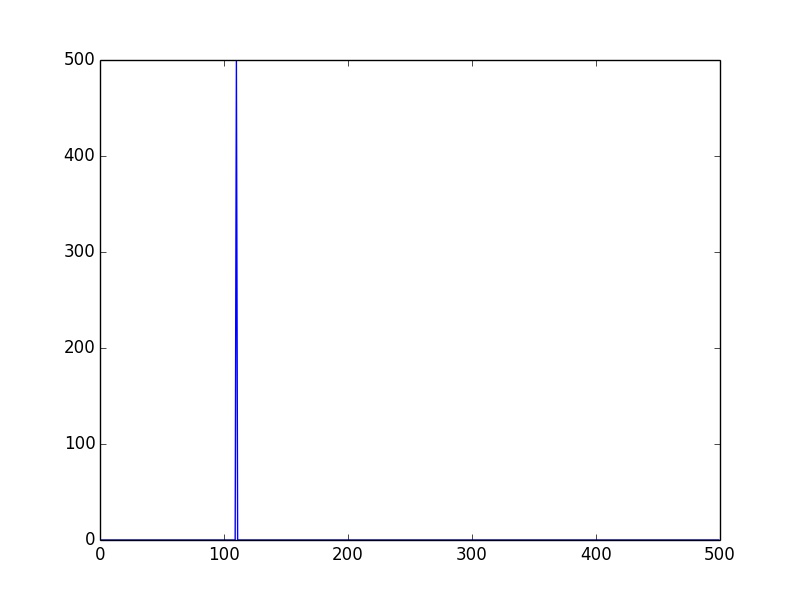

但是我们并不想对所有的x做fft,比如只取256个点,按理说得到的结果应该一样的,因为都是正弦信号,取哪部分计算频率都是一样的.

1
2
3
4
5
6
7
8
N = 256
f = 110
fs = 1000
x = numpy.sin(2*numpy.pi*f*numpy.arange(N)/fs)
X = numpy.fft.fft(x)
magX = numpy.abs(X)
plt.plot(magX)[:N/2]
plt.show()


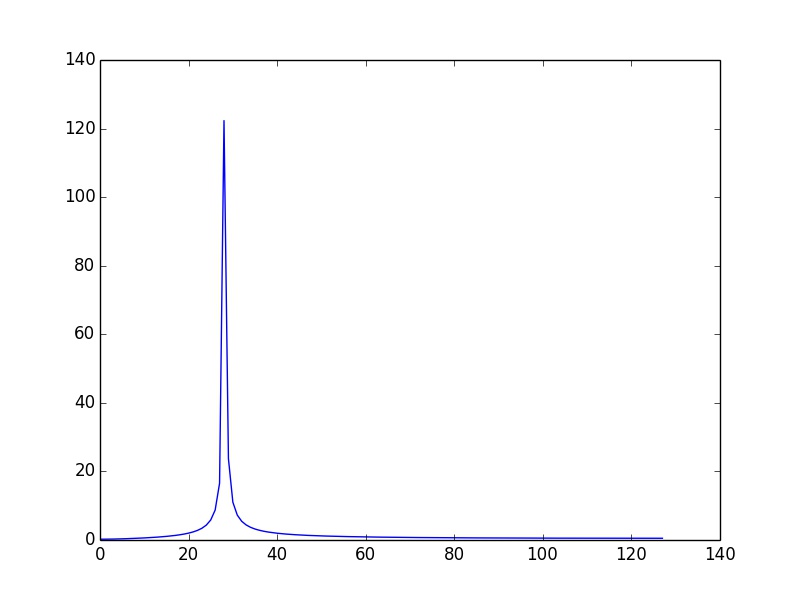
但是这样脉冲就不再110HZ上了..这时有还有一步,要给横轴频率乘上频率解析度 fs / N.

1
2
3
4
5
X = numpy.fft.fft(x)
magX = numpy.abs(X)
f_sequence = numpy.arange(X.size/2) * fs / N
plt.plot(magX[:N/2])
plt.show()

结果就对了.