高斯性的度量
高斯性是说一个分布,或者一组数据像不像高斯分布.先说一元高斯的度量.
一元高斯
q-q plot
Quantile-quantile plot实际上可以度量任意两种分布之间的相似性,以高斯分布举例.
Quantile是分位点,比如高斯分布的二分位点在高斯概率分布函数的中心,出现在二分位点之前的概率是50%,
十分位点是将高斯概率分布分成了10部分,每部分等概率(0.1),这些等分点就是分位点.如下图.
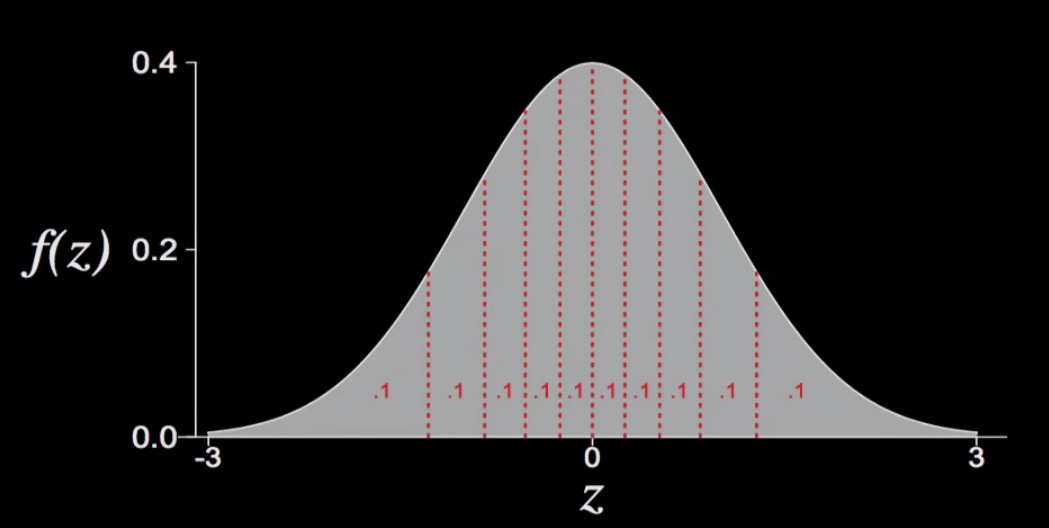
q-q plot步骤:
(1). 将待测数据从小到大排序(比如有9个数据).
(2). 找出标正态分布的十(9+1)分位点(对应着9个数).
(3). 以(1)的结果作为y,(2)的结果作为x画图.
如果数据是高斯的,那么这组数据(9个)就假设是从一个高斯中采样得来,应该会和9个十分位点接近.这样画出的q-q plot应该是条直线.如下图, 是90个数据画出来的.
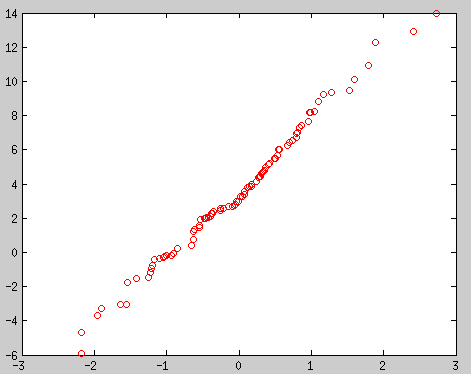
MATLAB的qqplot函数,可以不用以上步骤直接画出数据x和一个高斯分布的q-q plot,还拟合了条直线出来.下图是9个数据画出的.
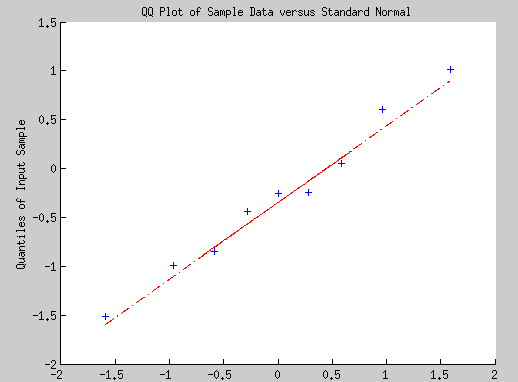
q-q plot的评估
如果数据是高斯的,那q-q plot应该接近一条直线.
如果非高斯,从q-q plot上也能推断出一些信息.如果下图,数据是从一个均匀分布里采样的.由于均匀分布不会出现很大或者很小的采样值,所以它在对应的区域是弯的.
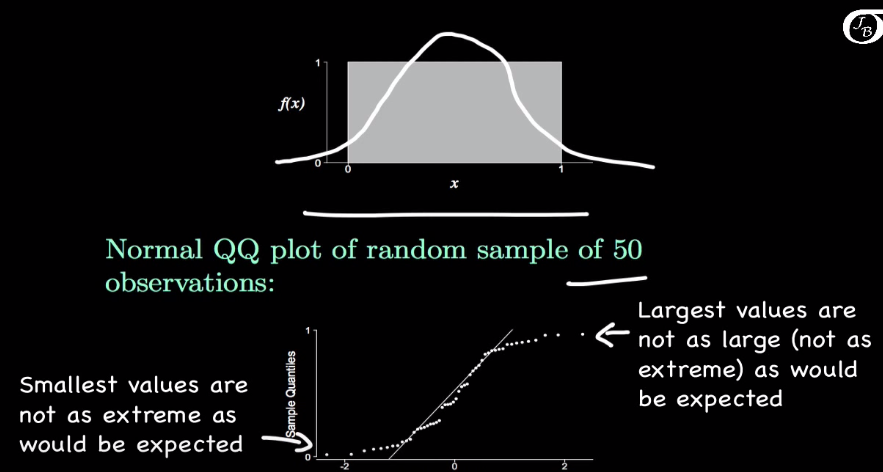
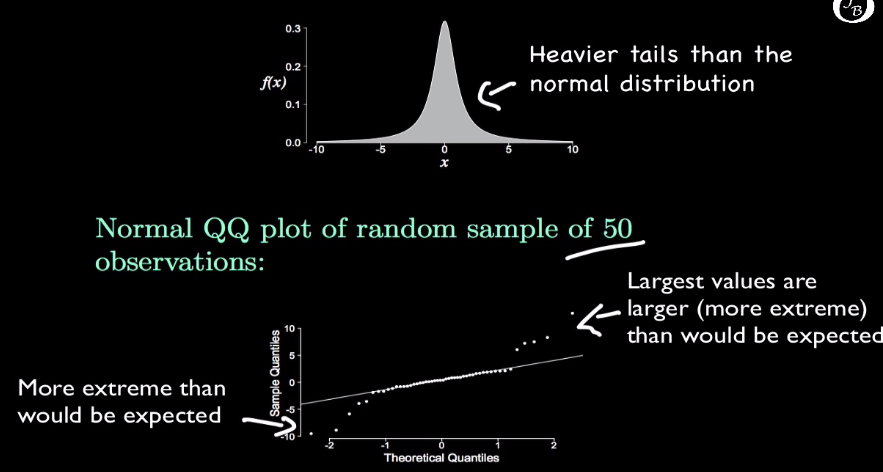
如果数据是从heavy-tail的分布,比如Laplace分布中采样的,它可能出现的最大值比高斯的大,最小值比高斯的小,所以对应区域也会弯曲,不过方向和均匀分布的不一样.
多维高斯分布
一维的高斯分布可以画出来,高维的就不行了.所以必须要得出一个一元的统计量,这个统计量一般是马氏距离( Mahalanobis distance).
马氏距离
$$D_M(x) = \sqrt{(x - \mu)^T S^{-1} (x-\mu)}.\, $$
x和u是n维向量,S是协方差nxn矩阵,马氏距离是一个一元统计量.
马氏距离和q-q plot
有人证明(见参考文献),如果一组数据来自一个多元高斯分布,那么它关于马氏距离D的统计量\(u = \frac{nD^2}{(n-1)^2}\)服从beta分布.这样又可以用q-q plot来验证了,只要统计量\(u\)和beta分布的分位点画出来接近一条直线,就能说明原始数据可能来自一个多元高斯分布.
参考文献
- N. J. H. Small, “Plotting squared radii,” Biometrika, vol. 65, no. 3, pp. 657–658, 1978.
- R. Gnanadesikan and J. R. Kettenring, “Robust estimates, residuals, and outlier detection with multiresponse data,” Biometrics, vol. 28, no. 1, pp. 81–124, 1972.
其他资料
https://www.youtube.com/watch?v=X9_ISJ0YpGw
MATLAB doc qqplot, quantile