2015-10-18

广义高斯分布的MLE拟合

---

MATLAB提供过了一些分布的拟合函数,对于常见分布直接使用即可,但这里面没有广义高斯分布和拉普拉斯分布.用分布拟合文档里推荐的MLE方法可以实现它们.
先来写个高斯测试一下,然后再验证广义高斯的拟合结果.

高斯分布

为了重复实验所以设置了random seed.

rng(1)
x = normrnd(8,3,1000,1);

x是1000*1的向量,服从均值为8,标准差为3的高斯分布.先用自带拟合函数计算.

>> [mu, s] = normfit(x)
mu =
       7.9602
s =
       2.9954

然后用分布函数和mle函数拟合.normpdf是自带的高斯密度函数.mle需要传入的参数有数据x,需要估计的密度函数的句柄,以及初始化参数.

>> [para_est] = mle(x,'pdf',@(x,mu,s)normpdf(x,mu,s),'start',[1,1])
para_est =
       7.9602       2.9939

广义高斯分布

MATLAB没有广义高斯分布的密度函数,需要手写.直接套公式.

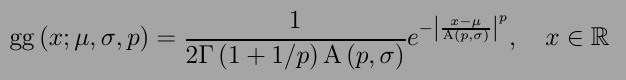
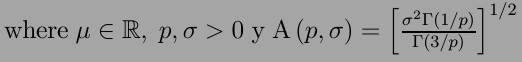
ggdpdf = @(x, mu, s, p) 1 / ( 2*gamma(1+1/p)*( s^2*gamma(1/p)/gamma(3/p) )^0.5 ) ...
                   * exp(-abs( (x-mu) ./ (( s^2*gamma(1/p)/gamma(3/p) )^0.5) ).^p);

[para_est] = mle(x,'pdf',@(x, mu, s, p)ggdpdf(x, mu, s, p),'start',[1, 1, 1])
para_est =
       8.0839       2.8851       1.9654

基本上是准确的.
但是有个问题,数据是1000*1的向量,这么多点,参数猜都猜出来了.试试把只用50个x来估计,果然出错了.

[para_est] = mle(x,'pdf',@(x, mu, s, p)ggdpdf(x, mu, s, p),'start',[1, 1, 1])Error using mlecustom>llf_pdfcdf (line 440)The PDF function returned negative or zero values.Error in fminsearch (line 309)    x(:) = xr; fxr = funfcn(x,varargin{:});Error in mlecustom (line 183)        [phat,nll,err,output] = ...Error in mle (line 229)            phat = mlecustom(data,varargin{:});Error in untitled2 (line 11)[para_est] = mle(x,'pdf',@(x, mu, s, p)ggdpdf(x, mu, s, p),'start',[1, 1, 1])

Error using mlecustom>llf_pdfcdf (line 440)
The PDF function returned negative or zero values.
Error in fminsearch (line 309)
    x(:) = xr; fxr = funfcn(x,varargin{:});
Error in mlecustom (line 183)
        [phat,nll,err,output] = ...Error in mle (line 229)            phat = mlecustom(data,varargin{:});Error in untitled2 (line 11)[para_est] = mle(x,'pdf',@(x, mu, s, p)ggdpdf(x, mu, s, p),'start',[1, 1, 1])
Error in mle (line 229)
            phat = mlecustom(data,varargin{:});
Error in untitled2 (line 11)
[para_est] = mle(x,'pdf',@(x, mu, s, p)ggdpdf(x, mu, s, p),'start',[1, 1, 1])

50个数据估计3个参数有点难,那估计两个呢.直接把样本均值作为分布中的参数mu,然后只估计标准差s和形状参数p.
新创建一个句柄,和ggdpdf一样只不过有了固定的均值参数.

x = normrnd(8,3,50,1);
x_mean = mean(x);
ggdpdf_u = @(x, s, p)ggdpdf(x, x_mean, s, p)
[para_est] = mle(x,'pdf',@(x, s, p)ggdpdf_u(x, s, p),'start',[1, 1])

para_est =
       3.0375       4.1631

这样倒是算出来了,标准差s还算准确,只是形状参数差的有点多.
去掉random seed后多次实验发现,s每次估计的都能够接受,形状参数p受数据影响波动较大,有时会偏的离谱,比如对高斯分布的数据会估计出6.
所以只能增加样本了.

Whatyouknowabout

Fitting, 高斯