2015-08-25

隐马尔可夫模型实现分词

最近看到几篇很好的博文介绍HMM,我想再参考数学之美上讲的,把HMM的第二问题实现一遍.一年前用HMM-GMM做过语音识别,但语音识别问题涉及知识太多,一段时间没做我也忘差不多了.其实没有GMM的HMM还是很简单的.

隐马尔可夫模型

维基百科上的例子是这样说的:每天,你的朋友有一定的概率进行下列活动:”散步”, “购物”, 或 “清理”. 每天的天气有两个状态,”雨”或”晴”.你的朋友根据每天的天气情况决定当天的活动.如果你的朋友告诉你他第一天散步,第二天购物,第三天清理,那么你能否通过他的活动来判断这三天的天气?将这个事件加上一定的假设,再用数学语言描述出来,这个数学模型就是HMM了.为啥叫HMM也很清楚,我们只能通过可见的观测来推断隐藏的状态.

首先这个问题有两个状态(“雨”或”晴”),三个观测(“散步”, “购物”, 或 “清理”),解决这个问题这些当然不够,所以我们得想办法得到一些先验知识.比如我们从气象台获取到这样的数据:任意一天下雨的概率,任意一天是晴天的概率等,在HMM问题里,这样的先验知识叫做初始概率.另外,又从气象台获得了许多这样的数据:如果当天下雨,那么第二天也下雨的概率;当天天晴,第二天下雨的概率等.这些我们叫做转移概率,也就是状态转移概率.最后,我们从朋友那里询问得到这样的数据:如果当天下雨,那么他”散步”, “购物”, 或 “清理”的概率等.这个叫做发射概率(注意,这个发射概率很有可能来自某种分布,如果假设它来自一个高斯混合模型,那么这就是HMM-GMM了).

有了这5组参数就能解决HMM问题了.总结一下:(这篇博客实现了Python版)

// 1. 状态集合:
string states[] = {"Rainy", "Sunny"};
// 2. 观测集合:    
string observations[] = {"walk", "shop", "clean"};    
// 3. 初始概率
map<string, double> start_probability;
start_probability["Rainy"] = 0.6;
start_probability["Sunny"] = 0.4;
// 4. 状态转移概率
/*  其实是一张表
    Rainy   Sunny
Rainy    0.7     0.3
Sunny    0.4     0.6    
*/
map<string, map<string, double>> transition_probability;
transition_probability["Rainy"].insert(make_pair("Rainy", 0.7));
transition_probability["Rainy"].insert(make_pair("Sunny", 0.3));
transition_probability["Sunny"].insert(make_pair("Rainy", 0.4));
transition_probability["Sunny"].insert(make_pair("Sunny", 0.6));
// 5. 发射概率
/*      walk    shop    clean
 * Rainy    0.1 0.4 0.5
 * Sunny    0.6 0.3 0.1
*/
map<string, map<string, double>> emission_probability;
emission_probability["Rainy"].insert(make_pair("walk", 0.1));
emission_probability["Rainy"].insert(make_pair("shop", 0.4));
emission_probability["Rainy"].insert(make_pair("clean", 0.5));
emission_probability["Sunny"].insert(make_pair("walk", 0.6));
emission_probability["Sunny"].insert(make_pair("shop", 0.3));    
emission_probability["Sunny"].insert(make_pair("clean", 0.1));

现在有这些数据能计算出什么?如果用$s_t$表示某一天的状态(第t天的天气),$o_t$代表某天的活动(第t天的活动),那么我们实际上最终想要得到的是这样一组$s_1,s_2,…s_N$,使得
$$P(s_1,s_2,…,s_N |o_1,o_2,…,o_N)$$最大,啥意思,就是朋友告诉了你他3天的活动,你要找出这3天的最可能出现的天气状态,让这个条件概率最大,这就是我们本来的问题.
上面这个条件概率可以化简,首先用一次贝叶斯公式,再加入马尔科夫性质(无时间后效性以及观测相互独立,具体看数学之美),这两步操作后问题就变成了希望找到一组状态$s_1,s_2,…s_N$,使得$$\prod P(o_i|s_i)P(s_i|s_i-1)$$最大(那个$i-1$是下标,不知道为啥显示不对).
这个问题就是HMM的第二问题,解决方法是使用Viterbi算法.
把上式画成图如下,是一个篱笆网络(lattice),它表示出了所有时间点上可能的状态,而存在一条最短路径使得上式最大.

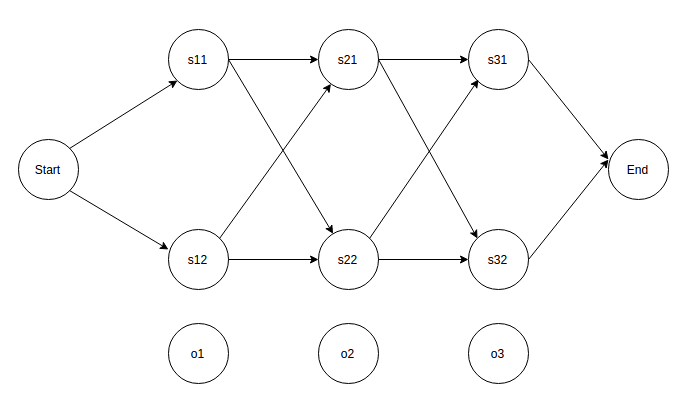
使用Viterbi算法可以计算出概率最大的路径,这需要借助两个辅助数组.
第一个数组weight记录的就是$P(o_i|s_i)P(s_i|s_i-1)$,所以维度是[2][3]—>[状态数][天数].
对于第1天,观测$o_1 = “walk”$,

1 2	weight["Sunny"][0] = start_probability["Sunny"] * emission_probability["Sunny"]["walk"]; weight["Rainy"][0] = start_probability["Rainy"] * emission_probability["Rainy"]["walk"];

对于第二天,观测是$o_2 = “shop”$,weight[“Sunny”][1]需要考虑前一天的状态到底是”Sunny”还是”Rainy” ,Viterbi算法总是选择算出来结果比较大的那一个.

weight["Sunny"][1] = 
weight["Sunny"][0] * transition_probability["Sunny"]["Sunny"] * emission_probability["Sunny"]["shop"] 
>  weight["Rainy"][0] * transition_probability["Rainy"]["Sunny"] * emission_probability["Sunny"]["shop"] 
? weight["Sunny"][0] * transition_probability["Sunny"]["Sunny"] * emission_probability["Sunny"]["shop"] 
:  weight["Rainy"][0] * transition_probability["Rainy"]["Sunny"] * emission_probability["Sunny"]["shop"] ;

另一个数组path用来记录路径,它表示的是对于所有可能的状态,在某个时间点上,它上一时刻是哪种状态.比如path[“Sunny”][1] = “Rainy”表示1时刻的状态是”Sunny”,它对应的那条路径的上一时刻(0时刻)的状态是”Rainy”.
weight和path计算完以后,考虑最后一个时间点,找出weight最大的那个对应的key,这个key表示Viterbi的最后一个状态是什么.如果是”Rainy”,那么就去查看path[“Rainy”][最后的时间点],这样就找到了上一个时刻的状态,再用这个状态去上一个时刻,一直back track到头,就找到了整个路径.
这个weight到底是什么,我参考的那篇博客上说是$P(时间,观测)$,我觉得不是这个,应该是记录的当前节点到开头节点的距离.
完整C++代码见这里.

参考:

Amnesia's blog

I'll be your mirror

隐马尔可夫模型实现分词

隐马尔可夫模型