---

在图像问题中对向量求导非常常见,比如经常会有这样一个步骤:

• 1.写方程(代价函数,或者误差),变量是x是把图片(矩阵)拉直了的向量.
• 2 方程关于x求导.
• 3 让导数为0,解x.
  下面总结一下经常碰见的几种情况.

1. \(y = x^T \times a\)

\(y = x^T \times a\), 或者\(y = a^T \times x\),其中 $$x = \left(\begin{array}{c}x_1\\ x_2 \\. \\. \\. \\x_n \end{array}\right), a = \left(\begin{array}{c}a_1\\ a_2 \\. \\. \\. \\a_n \end{array}\right)$$

这两种其实y一样,\(y = \sum_{i=1}^{n} x_i a_i \)是个标量.那么$$\frac{\text{d}y}{\text{d}x}=\left(\begin{array}{c}\frac{\text{d}y}{\text{d}x_1}\\ \frac{\text{d}y}{\text{d}x_2} \\. \\. \\. \\ \frac{\text{d}y}{\text{d}x_n} \end{array}\right) = \left(\begin{array}{c}a_1\\ a_2 \\. \\. \\. \\a_n \end{array}\right) = a $$

2. 二次型

$$x = \left(\begin{array}{c}x_1\\ x_2 \end{array}\right)$$

\[A = \begin{bmatrix}a11 & a12 \\ a12 & a22 \end{bmatrix}\]

注意A是个对称矩阵.A的二次型\[Q = x^TAx\]

$$\frac{\text{d}Q}{\text{d}x} = 2Ax$$
把二次型展开也很好推出这个结果.需要注意的是导数和求导的变量维度一样,比如\(\frac{\text{d}Q}{\text{d}x}\)和x一个维度,\(\frac{\text{d}Q}{\text{d}x^T}\)和\(x^T\)一个维度.

一个例子

某论文上一个问题,要解x,就是找使得下面方程最小的一个x(向量).也就是给这个方程对x求导,让导数为0.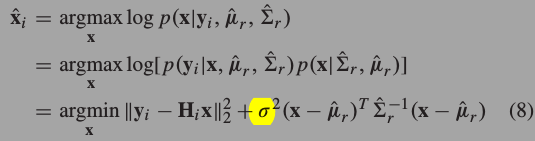

下面推一下,为了方便省略下标i和r和标记^.将方程写成两部分,分别求导.
$$|| y - Hx ||_2^2 \ (1)$$
$$\sigma^2(x-\mu)^T \Sigma^{-1} (x-\mu) \ (2)$$
(1)式即向量二范数平方,也就是square error,可以写成$$(y - Hx)^T(y - Hx)\\
= y^Ty - y^THx - x^TH^Ty + x^TH^THx
$$
求导得到$$-H^Ty-H^Ty+2H^THx$$
(2)式形式就是上面说的二次型,直接用公式得到
$$2\sigma^2\Sigma^{-1}(x-\mu)$$
合并起来就是$$\frac{\partial E(x)}{\partial x} =-2H^Ty+2H^THx + 2\sigma^2\Sigma^{-1}(x-\mu) = 0 $$
解出x,
$$x = (\sigma^2\Sigma^{-1} + H^TH)^{-1}(H^Ty + \sigma^2\Sigma^{-1}\mu)$$
和论文上一样.