[论文笔记]Nonlocally Centralized Sparse Representation for Image Restoration
Intro
图像恢复问题(Image Restoration)可以用一个式子表示:
$$
\begin{equation} \label{eq:someequation}
y = Hx + v
\end{equation}
$$
y是观测到的图像(即退化的图像),x是真实图像(理想化的真实),v是噪声,H称为退化矩阵.比如去模糊问题用上式表述就是:一张sharp的图像经过某种模糊H(大气涌动,失焦等),并且在成像过程收到某种噪声v污染,最终相机拍到的图像是y.
传统方法往往会使图像过分光滑(over-smooth),最近几年图像恢复问题大多引入稀疏表达的方法.
稀疏表达认为信号都是稀疏的,一个信号\(x \in \mathcal{R}^N\),被认为可以近似由一个词典中的内容拼成,即
$$x \approx \Phi \alpha$$
\(\Phi\)是词典,\(\Phi \in \mathcal{R}^{N \times M} (N < M)\), 由于M > N,这个词典成为过完备的.说到过完备,PCA的到的N个主成分也构成一个词典,它不是过完备的,具有很好的性质(各个成分相互独立,正交).由于稀疏表达的过完备词典,需要加入正则项才能求解出\(\alpha\),这些正则项的功能往往就是简单地让\(\alpha\)大多数为0,这样\(\alpha\)就是原始信号x的系数表达.
\(\alpha\)最直观的解法是这个方程,由于那个L0范式让这个问题成了NP-hard,所以一般不解这个式子.
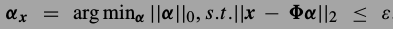
有人证明L1范式优化的结果和L0差不多,L1可以解,与是换成了下式.
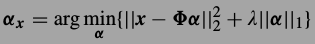
图像恢复问题中,我们能观测到的图像y都是退化后的(通过最上面的式子),要从y恢复出x,首先要把y稀疏表示了.也就是求解下式:
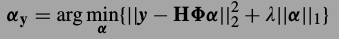
然后真正的x可以由
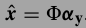 重建.这个意思是如果\(\Phi\)是能够表达x的词典,那么\(H \Phi\)就是能表达退化图像y的词典了.由于上式能够使
重建.这个意思是如果\(\Phi\)是能够表达x的词典,那么\(H \Phi\)就是能表达退化图像y的词典了.由于上式能够使 ,那么就能够认为
,那么就能够认为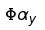 也就是真实的x了.
也就是真实的x了.这篇文章作者观察到,稀疏编码不是随机分布的,是和图像本身非常相关,于是试图利用图像中的局部与非局部冗余信息来建立更好的稀疏模型.
##稀疏编码噪声(Sparse Coding Noise, SCN)
为了让优化得来的\(\alpha_y\)接近真实的\(\alpha_x\),作者用SCN表示两者的偏离,目的就是减少SCN.
SCN的式子:
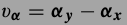
SCN减少意味这x恢复的准确,因为 $$\widetilde{x} - x \approx \Phi \alpha_y - \Phi \alpha_x$$
$$\Phi \alpha_y - \Phi \alpha_x = \Phi v_a$$
Nonlocally Centralized Sparse Representation (NCSR)
词典都是由小的图像片训练的.x是一个大图像展成的N维度向量,从位置i出截取一个小图片块\(x_i\),方法是
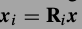 ,小图片块是\(\sqrt(n) \times \sqrt(n)\),\(x_i\)长度n.
,小图片块是\(\sqrt(n) \times \sqrt(n)\),\(x_i\)长度n.词典为
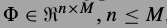 ,小图片块可以表示为
,小图片块可以表示为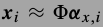
小图片块的稀疏表达系数可解
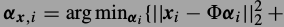
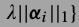 得到.如果的到了所有位置处的小图片的系数,那么整张大图片可由下式恢复.这是一个最小二乘解.
得到.如果的到了所有位置处的小图片的系数,那么整张大图片可由下式恢复.这是一个最小二乘解.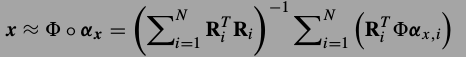
按照上式的标记法,要解决的问题就是求解下式
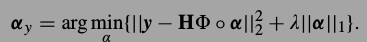
观察\(v_{\alpha}\)的性质
作者通过实验观察到了\(v{\alpha}\)可以很好地用Laplacian分布描述.这张图看的不是很懂,文中说这是distribution of \(v{\alpha}\) corresponding to the 4th atom,是说\(v_{\alpha}\)的第4项的分布吗?
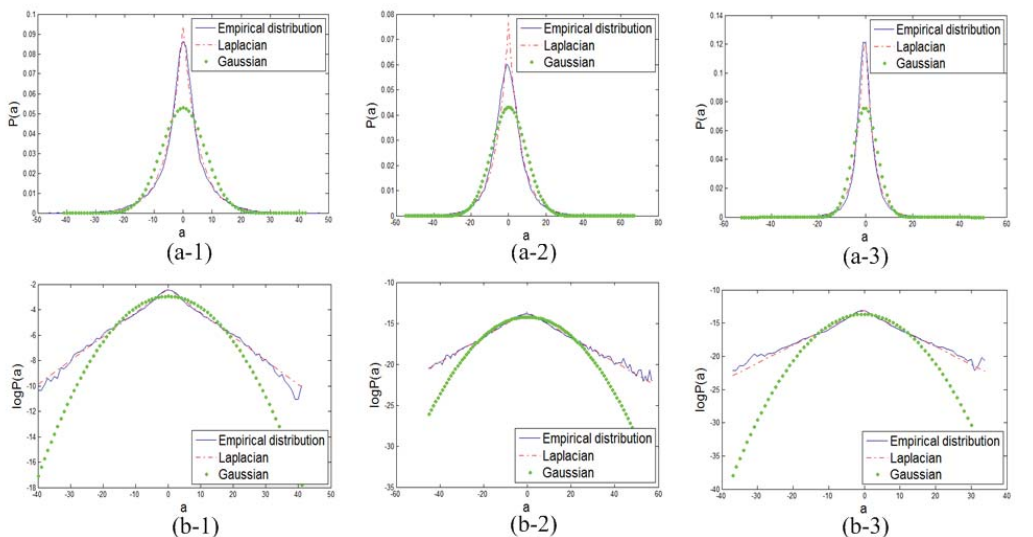
###NCSR模型
由于\(\alphax\)不知道,所以\(v{\alpha}\)也没办法得到.那就再对\(\alpha_x\)进行估计,记为\(\beta\),让\(\alpha_y - \beta\)作为SCN的估计,与是就有了下式,加入了对\(\beta\)的估计,让每一个局部的\(\beta_i\)接近\(\alpha_i\),所以这个式子称为centralized sparse representation.
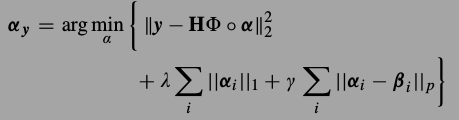
然后就是如何选择,如何构建词典了.DCT,小波之类无法足够描述图像系细节,KSVD可以训练通用词典,能够更好地描述图片结构.但是实验发现过完备词典得到的稀疏编码是不稳定的,就是说虽然两个图像片很很像很像,但他们的编码却差别很大.相比之下PCA的到的编码就比较稳定.所以这篇文章用了KPCA,很巧妙的方法,来构建过完备词典.具体是,对所有的图像片使用K-MEANS进行聚类,对每个类里的样本通过PCA的到一组完备基,这样把K组拼起来就是词典了.这样的词典具有天生的稀疏表达特性,因为对任意一个图片,通过聚类就能在K类里选出一个类,使用这个类对应的基就能表示,其他组系数都为0即可.这篇文章只使用输入图片本身来构建词典.这样就可以把以前式子中的引入稀疏性质的正则项去掉.新的优化方程为
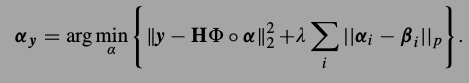
如果p=1,那么这个式子就是词典学习的标准式子,第一项表示重建相似度,第二项是一个一范数,作为引入稀疏性质的正则项.
那么NCSR的N,nonlocally是从哪里来的?就是对\(\beta\)的估计,是使用周围的图像片来做的,具体在后面的算法中.
###对未知稀疏编码的非局部估计方法
\(\beta\),即对\(\alpha_x\)的估计.由于使用了PCA作为词典,这样得到的编码比较稳定,另一方面由于图片自身有很多冗余信息(很多结构重复出现),所以就产生了使用非局部图像片估计的方法.其实就是在给定的位置i周围去寻找相似的图像片,为了找的更加准确,还引入了多尺度的方法(大概是指在缩放的图像片上寻找相似的).估计就是对这些相似图相片的稀疏编码做权值求和.
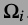 是相似图片块的集合,\(\beta_i\)可以表示为
是相似图片块的集合,\(\beta_i\)可以表示为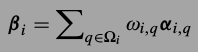 ,其中
,其中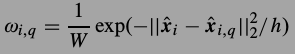 .权值是距离的反比.PCA作为词典真是很方便,它的稀疏编码就是在新方向上的投影,
.权值是距离的反比.PCA作为词典真是很方便,它的稀疏编码就是在新方向上的投影,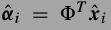 ,
,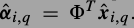 .
.整个优化过程是一次一次的迭代,来解目标方程
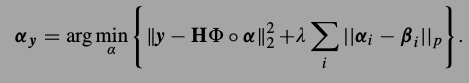
具体地,首先给\(\beta_i\)一个初始值,用解上式的标准方法解出一个\(\alpha_y\),然后就有了x的估计,有了x的估计就可以在位置i附近找非局部的图像片,用权值和的方式估计一个新的\(\beta_i\),并且认为这个新的\(\beta_i\)变得准确了,那么就用这个新的估计进行下一次迭代,直到收敛.论文原话是这样说的, Finally, the desired sparse code vector α y is obtained when the alternative optimization process falls into a local minimum.这句话说的相当准确.虽然这个算法不像一些算法能找到global minimum,但这个全局最小值是否是真正要找的最小值?不确定.相反地,有些局部最小值往往更有可能接近最优解.
##NCSR概率解释
这个算法还可以从概率角度解释,这个解释也可以用来对算法中的超参数进行选择.大概就是先记
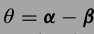 ,对于\(\theta\)的MAP估计为
,对于\(\theta\)的MAP估计为
其中第一项
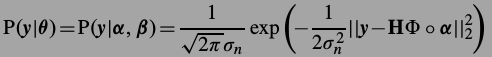
第二项,也就是SCN,通过前面的观察,认为它是Laplacian分布,
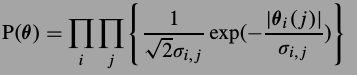
进行替换,得到