Normal equation和Least squares以及最小二乘法拟合圆
最近一个月三次碰到normal equation,本来不打算管这个了应为梯度下降就能解决同样的问题,但还是总结一下吧.
第一次碰到normal equation是Andrew Ng的ML公开课,讲线性回归的那章.第一种做法是写出误差函数
\[J(\theta) =\frac{1}{2m} \sum_{i=1}^m(h(x) - y)^2 \]
其中\(h(x)\)是关于\(\theta\)的函数.Ng说除了使用梯度下降法来得到一组\(\theta\)使得误差函数最小,还有一种矩阵分析的方法,不需要迭代直接可以算出满足条件的\(\theta\).
$$\theta = (X^T X)^{-1}X^T y$$
这个式子叫做Normal equation.X是所有样本的各个取值组成的矩阵,y是样本对应的目标值组成的向量.Ng没有在公开课上证明这个式子.
第二次碰到是在Bengio的Deep learning里,还是在线性回归的例子里,他使用这个式子作为误差度量P
$$MSE_{test} = \frac{1}{m} || \hat{y}^{(test)} - y^{(train)} ||^2 _2$$
即mean squared error,然后对于\(MSE_{test}\)求关于参数w(这个w和上面的\(\theta\)一样)的偏导,便能推到出和Ng说的那个Normal equation.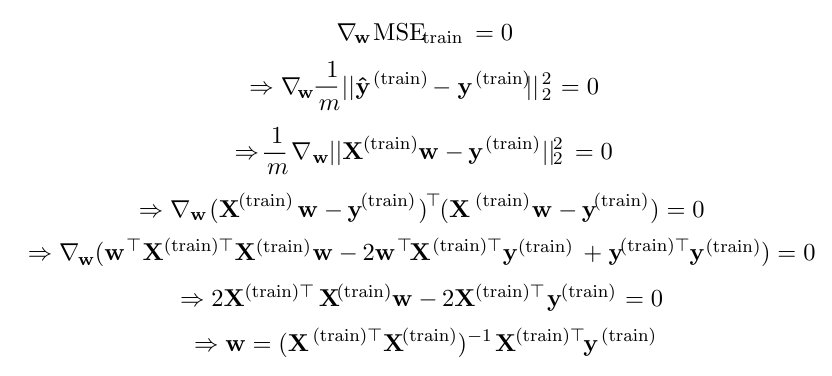
然后第三次碰到是上周的矩阵课,一个月没去了,去了意外发现原来这个Normal equation的出处在这里,它就是最小二乘问题…
上面那个代价函数\(J(\theta)\)和误差函数\(MSE_{test}\),都是在解最小二乘问题.按书上:当线性方程组\(A\vec{x}= \vec{b}\)无解时,希望找到这样的向量\(\vec{x}_0\),使得\( ||A\vec{x}_0 - \vec{b}||_2 = min ||A\vec{x} - \vec{b}||_2\),这样的解\(\vec{x}_0\)叫矛盾方程组(因为它实际上是没有解的)\(A\vec{x}-\vec{b} = 0\)的最小二乘解.证明方法是直接对这个范式展开关于向量\(\vec{x}\)求导,得极值为0的向量便是所求,表达式就是上面那个Normal equation解.
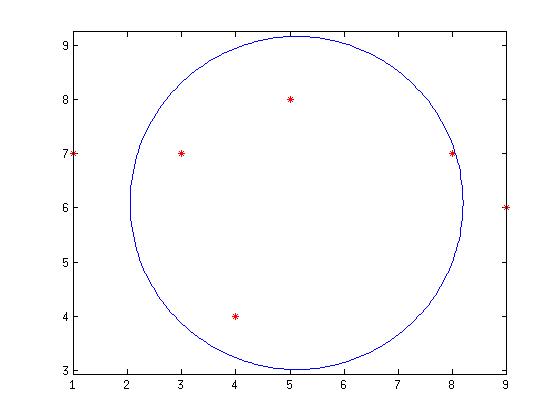
上面机器学习举例全是线性回归,但最小二乘能做的很多不只是拟合直线,它还能拟合非线性的函数,比如圆.如果我们要根据一些点来拟合出一个最合理的圆,最合理简单说就是希望这些点尽可能的在这个圆的周围.比如圆的方程是这样$$(x-a)^2 + (y-b)^2 = R^2$$
a,b,R是我们要找的圆心的横坐标纵坐标和半径,”最合理的圆”用数学表达式写出来就是这样$$argmin(a,b,R) \sum_{i=1}^m (x_i-\hat{a})^2 + (y_i -\hat{b})^2 - \hat{R}^2 $$ \((x_i,y_i)\)是所取的第i个点的坐标,这个式子和上面那两个线性回归问题的代价函数很像,实际上它就是一个最小二乘问题,要是给这个式子加个根号就和书上的最小二乘写成范数的定义一样了.现在想办法把这个式子展开写成\(A\vec{x}=\vec{b}\)的样子.
展开\((x-a)^2 + (y-b)^2 = R^2\)然后移项,可以拼出这样的式子
$$2x_i\hat{a} + 2y_i\hat{b} - (\hat{a}^2 + \hat{b}^2 - \hat{R}^2) = x_i^2 + y_i^2$$
令\(A= \left( \begin{array}{ccc}
2x_1 & 2y_1 & -1;\
… & … & …;\
2x_m & 2y_m & -1;\end{array} \right) \)大小是m*3维,m是取的点的个数,令\(\vec{x} = \left( \begin{array}{ccc}
\hat{a} ; \hat{b} ; \hat{a}^2+\hat{b}^2-\hat{R}^2 \end{array} \right) \),大小是3*1;令\(b = \left( \begin{array}{ccc}
x_1^2+y_1^2;…;x_m^2+y_m^2 \end{array} \right)\),大小是m*1维,这样上面的”最合理的圆”就可以写成\(A*\vec{x} = \vec{b}\),\(\vec{x_0}\)就是我们要找的最小二乘解,它是圆方程的一组参数.
matlab代码1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16xy_i = [8,7;4,4;5,8;1,7;9,6;3,7];%随便找了6个点
x_i = xy_i(:,1);
y_i = xy_i(:,2);
n = length(xy_i);%A维度应该是6*3
A = [2*x_i,2*y_i,-1*ones(n,1)]
b = [x_i.^2 + y_i.^2] %b维度应该是6*1
para = A \ b; %para是圆方程的参数,这里直接用了除,写成normal equation是一样的
%para = pinv(A'*A)*A'*b;
a = para(1);b = para(2);R = sqrt(a^2+b^2-para(3));
plot(x_i,y_i,'r*')%画点
hold on
alpha = 0:2*pi/200:2*pi;%画圆
x = R*cos(alpha) + a;
y = R*sin(alpha) + b;
plot(x,y)
axis equal