PCA,Principal Component Analysis,主成分分析,是一种简单粗暴有效的数据降维方法.

介绍它是因为觉得PCA的想法很有意思,得到的结果非常直观.06年Hinton的Deep Belief Networks就是和PCA的结果做了对比.下次把Hinton的DBN介绍下.

PCA的目的就是数据降维,至于为什么降维,主要原因有这么几个:

• 高维数据中有冗余信息.比如有两列数据,一个是用cm表示的身高,一个是用inch表示的身高,这两列明显相关,所以可以省去一列.
• 高维数据有效的转为低维数据后,可以减少存储空间,提高算法的执行速度.
• 维度越高的数据,在算法设计的时候就要针对这么高维的数据做出更多的假设条件,容易造成最终的训练结果过拟合.
• 用于数据可视化.把高维数据降到二维或者三维就能比较直观的看出数据的分布或者样本之间的关系.

好了,先来最直观的2D降到1D.下面左图,是一堆二维数据,或者叫做二维特征,我们想用一维的特征来表示这些样本点,并且能够最大程度上保留以前这些样本的分布特点.以前的二维特征,看起来表示的意思就是这堆数据有的离的远,有的离的近,这很明显是可以降低到1D空间上的,做个投影就行了.比如下面右图,随便画一条线,每一个样本点在这条线上做投影,这样二维特征就全部降低到一维空间中了.

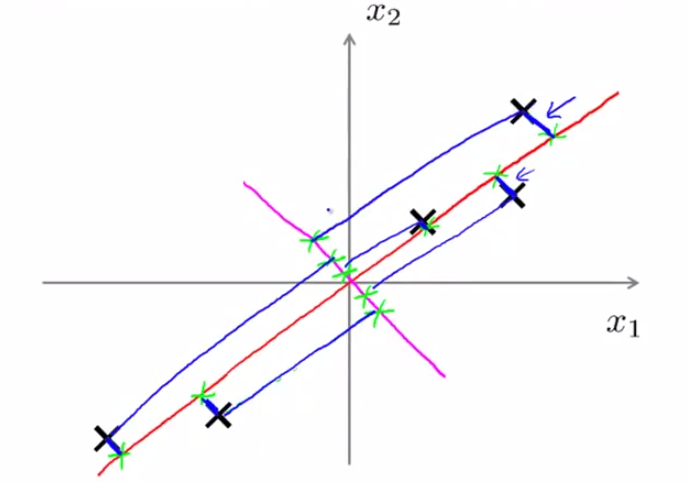
但是应该选怎样一个向量来做投影呢?如果选择上图中紫色的那条,可以是可以,但最后投影得到的点都挤在一起了,而红色那个向量做出的投影,各个样本点分散的很开.所以PCA的基本思想来了,就是首先计算样本点在哪个方向上变化波动最大,然后把数据投影到这些变化波动最大的方向上去.设我们要找的向量是\(\vec{u}\),限制\(\vec{u}\)为单位向量,一共有m个样本点,用数学表达式表述上面的思想就是$$max_{\vec{u}:||\vec{u}||=1} \frac{1}{m}\sum_i^m (x^{(i)T} \vec{u})^2$$

$$max_{\vec{u}:||\vec{u}||=1} \vec{u}^{T} \frac{1}{m} \sum_i^m x^{(i)} x^{(i)T} \vec{u}\qquad(1) $$

意思是所有样本的投影平方和最大,想想上面红色的线和紫色的线,那个对于所有样本的投影平方和比较大?明显是红色那条.写成这样之后,记\(\Sigma = \frac{1}{m} \sum_i^m x^{(i)} x^{(i)T}\),\(\Sigma\)实际上就是m个样本,每个样本维度是n,组成的n*m的矩阵X的协防差矩阵,大小是n*n.对(1)式,将限制条件\(\vec{u}:||\vec{u}=1||\)考虑,用拉格朗日方法求(1)右边部分最大值,就能发现\(\vec{u}\)就是\(\Sigma\)的特征值最大的特征向量.特征向量的方向就是我们要投影的方向.
证明是这样的:
$$goal: \qquad max: \vec{u}^{T} \Sigma \vec{u} \qquad constrain: \vec{u}^{T} \vec{u}=1 $$
$$Lagrange\quad function:L(\lambda,\vec{u}) = \vec{u}^{T} \Sigma \vec{u} + \lambda(\vec{u}^{T} \vec{u}-1)$$
$$\frac{\partial L}{\partial \vec{u}} = \Sigma \vec{u} - \lambda \vec{u} = 0$$
写到这就能看出来了,\(\vec{u}\)就是\(\Sigma\)的特征向量,而且是特征值最大的那个.为啥是最大的那个?我们不是要让\(\vec{u}^{T} \Sigma \vec{u}\)最大吗?\(\vec{u}^{T} \Sigma \vec{u} = \vec{u}^{T} \lambda \vec{u}\),当然\(\lambda\)越大越好.
于是PCA的使用就可以写成如下算法:

• 1.对m个样本构建样本矩阵X
• 2.计算X的协防差矩阵\(\Sigma\),以及\(\Sigma\)的特征向量和特征多项式.
• 3.如果最后要得到的数据是k维的,就选择特征值按大小排序前k个特征值对应的特征向量,组成一个矩阵\(Urecude\),用这k个特征向量作为基底,将原来的n维数据投影到k维上.做法是 z = Ureduce * x,这就是在计算每一维的投影.\(z\)是k*1维.

下面是coursera machine learning上使用PCA对人脸数据进行降维的例子.这是人脸数据库中的100张图片.

每个人脸有32*32=1024个像素点,每个点用一个灰度值来表示.所以这张人脸就可以看作是1024维空间中的一个向量.这个实验里提供了5000张图片,就是有5000个向量,我们希望找出个5000个向量所组成的数据,在哪些方向变化波动最大,然后把1024维向量投影到低维向量上去(实验中是100维).

来看看特征值最大的36个特征向量是些什么东西.特征向量大小是1024*1,把它reshape成32*32,再显示出来就是这样了.这36个特征向量就相当于人脸的36个最重要的特征,不同人脸的差别就反映在这些差别上,所以这些也叫做特征脸(eigenface).

实验里选择了前100个特征向量作为特征脸,or基底,也就是说每个样本从1024维降到了100维.怎么知道PCA的效果到底怎么样呢?想想一直到这一步PCA所做的事情.PCA是非监督学习,它根据很多很多样本来得到样本在哪些方向上变化最大,得到了一个由许多特征向量组成的降维矩阵Ureduce,通过z=Ureduce*x来降维.那么要恢复数据就只需要执行\(x_{reconst} = Ureduce^{-1} * z\)就行了,不过由于当时我们推导的时候限制了\(\vec{u}:||\vec{u}||=1\),所以这样得到的Ureduce的逆(这里是一般形式的矩阵的逆,就是伪逆)和Ureduce的转置是一样的,只用用Ureduce的转置乘以降维后的特征z就能恢复出x,当然x是有损失的,可以看作是x的估计.

这个损失有多大呢?看下最初的那些2D to 1D,再恢复到2D的例子,下图红色的点是恢复的点.

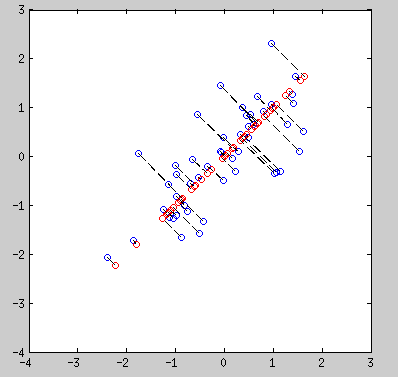
可以看到,由于我们只用了一个特征向量,所以我们恢复的数据全部落在这个特征向量上,损失掉了另一个方向(另一个特征向量方向)的波动变化,但仍然很好的反映了原始数据的特点.

下面是用100维数据恢复得到的1024维数据的图片,可以看到一些损失但不大.

下次补上牛逼哄哄的DBN,Hinton也是在这个人脸数据库上做的实验,看看DBN如何完虐PCA吧.