假设函数和代价函数及梯度

softmax回归是逻辑斯蒂回归的推广,即,逻辑斯蒂回归只能区分两个类,softmax回归将它推广到了k个.
这东西听着这么简单,因为逻辑斯蒂回归就那么简单,但是大牛们一直在用,放在各种神经网络的最顶层当作分类器.

---

逻辑斯蒂回归的假设函数和代价函数是这样的:$$\begin{align} h_\theta(x) = \frac{1}{1+\exp(-\theta^Tx)} \end{align} $$

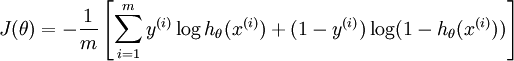
推广到k个分类,就是这样了:

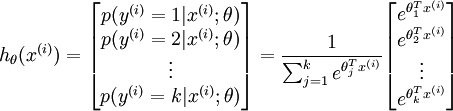
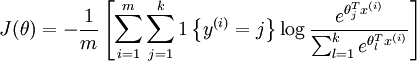
代价函数关于每个softmax 参数的梯度是

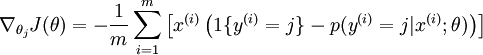
然后基本上就可以用数值优化方法(比如L-BFGS)里去迭代了.但还有个问题,因为假设函数是指数的,softmax会有一些奇特的性质,比如下面这个式子:

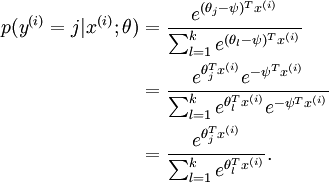
即它的参数同时加上一个常数结果不变,那就有很多组满足条件的参数了,这个叫做overparameterized.如果这样就去迭代会出现问题,所以在代价函数里加入了权值衰减项,问题就解决了.

---

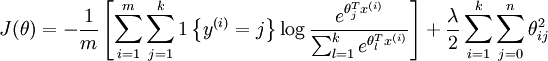
softmax回归和k个逻辑斯蒂回归,什么时候使用?

逻辑斯蒂回归也作为k类分类器,只要训练k个就行了.但是使用那个还得看情况.

直接把UFLDL教程上的例子搬过来.是说,如果k个类互相排斥,就用softmax回归;如果不互相排斥,就用k个逻辑斯蒂回归.

音乐分类:按照古典,乡村,摇滚,爵士来分,就用softmax;按照人声,舞曲,配乐,流行来分,就用k个逻辑斯蒂回归.

实验

直接使用MNIST的28*28=784维的向量作为输入,10个神经元作为分类,就是softmax回归了,直觉用类似训练逻辑斯蒂回归的方法来训练.