PCA的原理在这篇文章里以及记录,

这篇加上和PCA类似的ZCA白化.

---

PCA的另一种解释

使用PCA时,计算了一个协方差矩阵的各个特征向量组成的矩阵U,
$$ \begin{align} U = \begin{bmatrix} | & | & & | \\ u_1 & u_2 & \cdots & u_n \\ | & | & & | \end{bmatrix} \end{align} $$
如果要做PCA降维的话,比如要降到k维度,就选择上面那个矩阵u的前k列,作为一个Ureduce,用z = Ureduce * x就可以得到一个k维的向量.这个是PCA的一种解释,或者说实施,是Ng机器学习公开课上用的.在这个教程上他用了另外一种解释.如下.

---

如果用上面整个的矩阵U去乘一个向量x,得到的还是n维向量,和x一样,它其实是经过旋转过的x的表示,新得到的这个向量的基底就是矩阵U里的每个列向量,也就是用那些特征向量做为基底了.
$$ \begin{align} x_{\rm rot} = U^Tx = \begin{bmatrix} u_1^Tx \\ u_2^Tx \end{bmatrix} \end{align} $$

我们已经知道了这些数据在这些基底上的变化程度,在第一个基底上变化最大,然后依次减少.意思就是我们新的到的这个\(x_{rot}\)最后几维很小,那么直接就可以省去了.

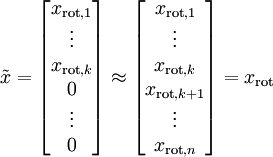
由于这个向量后面全是0,就直接可以省去当作一个k维向量,这就降维了,和最初那个方法一样.恢复数据的时候,把这个向量后面补上0,再去乘那个矩阵U的转置就变回去了.

---

在图像上应用PCA时,应该对每副图像单独做一个归一化处理,就是先计算这副图像的intensity均值,然后每个像素点的值减掉这个均值.
$$\mu^{(i)} := \frac{1}{n} \sum_{j=1}^n x^{(i)}_j \\
x^{(i)}_j := x^{(i)}_j - \mu^{(i)}$$

---

ZCA白化

如果想让信号的每个分量变得不相关,并且都具有相同的方差,就要用到白化.实际上我们之前计算的旋转过的表示\(x_{rot}\)已经具有了这个性质,下面是一个例子,这些二维点的协方差矩阵是这样的
$$\begin{align} \begin{bmatrix} 7.29 & 0 \\ 0 & 0.69 \end{bmatrix}. \end{align} $$
再给经过下面这一步,得到的协方差就是单位阵了.

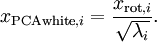
再经过下面这一步,就得到了ZCA白化,结果的协方差依然是单位阵.

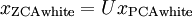
ZCA白化的结果最接近原始的信号,只是有了更好的性质.