推荐系统中的矩阵补全算法
最基本的问题,以用户电影评分为例,也就是这个用户-电影矩阵.

表中是用户多电影的评分,但评分有缺失,因为用户不可能对所有电影作出评价.
那么推荐问题就是给用户合理推荐一个没看过的电影,合理是指,预测用户应该对这部电影评分较高.然后这个问题就变成了矩阵补全,也就是填充表中的问号.
低秩矩阵分解
矩阵的补全有无数种可能,所以如果不对用户-电影矩阵(记为Y)的性质作出一定假设,那这个恢复问题就不可能完成.所以首先作出的假设是Y是低秩的.如果Y是低秩的,那么Y就能够由两个较小的矩阵线性组合而来.即:
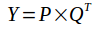
假设Y矩阵维度\(n_m \times n_u\),即有\(n_m\)部电影和\(n_u\)个用户,P的维度是\(n_m \times K\), Q的维度是\(n_u \times K\),K是特征的维度,也就是Y的秩.上式如果画出来就是这样.
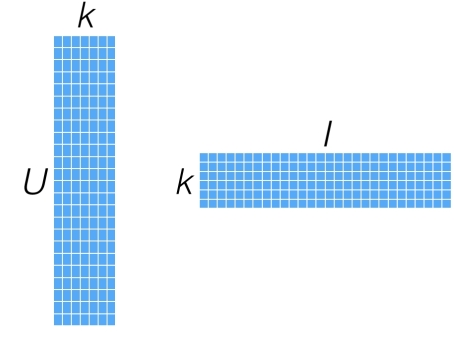
这表示了一个电影对应一个K维特征,一个用户对应了K个参数,反映出有用户对电影的K维特征的喜好程度.然后每个评分都可以看做是用户参数和电影特征的点积.试想如果我们得到了P和Q两个矩阵,我们就能对Y矩阵中的缺失值进行预测.
以上问题可以用梯度下降来求解,因为我们可以构造误差函数,并能计算偏导.

这个误差函数的意义是对于Y矩阵中存在的值,用P和Q乘积计算出预测值,让它们之间误差最小.当然,还加入了针对P和Q的L2正则项.这个误差函数对P和Q中每一项的偏导如下:
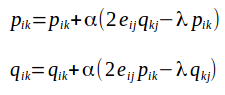
然后迭代求解即可.
协同过滤
这个算法本质上和低秩矩阵分解一样,但它里面的K维特征具有现实意义.一个电影的K维特征,就是它对应于K种电影风格的分量,比如只有两种风格的时候:
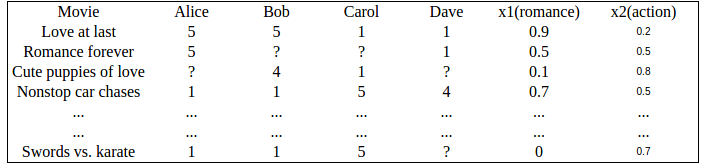
设一个电影的k维特征向量为\(x = [x_1, x_2,…, x_k]\),那么就应该存在一个用户参数向量\(\theta = [\theta_1,\theta_1,…,\theta_k,]\).这实际上和矩阵分解里的P和Q意义相同.
但实际情况是,这个电影特征无法得到,还是要通过迭代算出来.针对电影特征和用户参数,对应了两个代价函数.
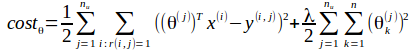
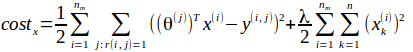
再分别求导,用梯度下降迭代至收敛即可.
核范数矩阵补全
这个方法的来源是一帮搞图像的科学家.图像恢复里经常有这种问题,比如图像被随机采样,试图从随机采样的图像恢复出原图.
首先它将问题定义为,认为用户-电影矩阵是由一个完全矩阵A下采样而来,而且还加上了噪音.L就是那个下采样变换.
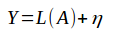
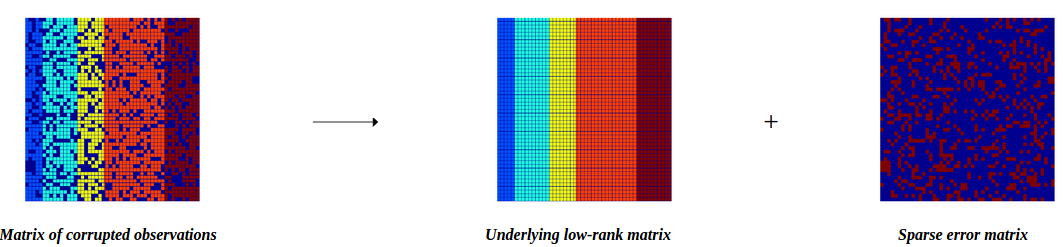
然后问题的解就是要求秩最小,如下:
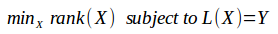
但直接去优化秩太困难了,于是换成了核范数,核范数就是矩阵的奇异值之和.
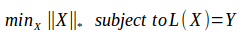
总结
这三种方法很类似,就是做出了Y矩阵低秩的假设.
前几天看了一篇文章推荐系统的那点事,觉得这些算法其实没多大用,虽然解决的是推荐系统的基本问题,但现实情况不是这么简单.